设A,B为n阶实矩阵，下列结论不成立的是【 】
A、 r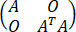
=2r(A)
B、r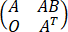
=2r(A)
C、r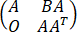
=2r(A)
D、r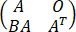
=2r(A)
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设A，B都是n(n≥2)阶复方阵，则rank(AB)=rank(BA).
已知n阶矩阵A,B,C满足ABC=0，E是n阶单位矩阵，记矩阵,,的秩分别为γ1,γ2,γ3，则【 】
设A是n阶方阵(n≥2),A*为A的伴随矩阵，(1)证明：|A* |=|A|n-1;(2)证明：R(A* )=.
设A是4×3矩阵，且A的秩r(A)=2，而B=，则r(AB)=________.
设A=，其中a_i≠0,b≠0(i=1,2,⋯,n)，则矩阵A的秩r(A)=________.
设A是n阶矩阵，A*为A的伴随矩阵，证明秩R(A*)与R(A)之间满足R(A* )=
设A为m×n且秩为s的矩阵，X为p×m的列满秩矩阵，即r(X)=m，而Y为n×q的行满秩矩阵，即r(Y)=n。证明：r(A)=r(XA)=r(AY)=r(XAY)其中符号r(T)表示矩阵T的秩。
设A是n阶正定矩阵，B为n阶实方阵，证明：(1)若B'=B,则AB的特征值为实数；(2)若B正定,则AB的特征值皆大于0；(3)若B正定,且AB=BA,则AB正定。
设A是n阶正定矩阵，E是n阶单位矩阵，证明A+E的行列式大于1.
设A为实对称矩阵。证明当实数t充分大之后，tI+A是正定矩阵，其中I表示单位矩阵。
设A,B均为n阶实对称阵，A的特征值均小于a，B的特征值均小于b.证明：对任意的k>a+b,A+B-kE是负定矩阵.
设A=(aij)n×n为正定矩阵.证明：f(x1,x2,…,xn )=是负定二次型，其中符号|∙|表示行列式.
设A=为n×n正定矩阵，证明：|A|≤a11 a22…ann.其中符号|∙|表示行列式.
设A是n级实对称矩阵，证明rank(A)=n的充要条件是：存在实对称矩阵B使AB+B'A是正定矩阵。
设S1,S3为实对称矩阵，S2为实矩阵，则矩阵S=为正定矩阵的充要条件为矩阵S3与矩阵S1-S2 S3-1 S2'皆为正定矩阵。
设A,B为n阶可逆矩阵，E为n阶单位矩阵，M*为M的伴随矩阵，则=【 】
设A,B,C,D都是n×n矩阵，且|A|≠0,AC=CA，证明=|AD-CB|.
已知矩阵A=，若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵，则P,Q可以分别取【 】
对数螺线ρ=eθ在点(ρ,θ)=(eπ/2,π/2)处的切线的直角坐标方程为__________.
设直线l:在平面π上，且平面π与曲面z=x2+y2相切于点(1,-2,5)，求a,b的值.
设函数f(u)具有二阶连续导数，而z=f(exsiny)满足方程∂2z/∂x2+∂2z/∂y2=e2x z,求f(u).
求[sin(π/n)/(n+1)+sin(2π/n)/(n+1/2)+⋯+sinπ/(n+1/n)]
已知二次曲面方程x2+ay2+z2+2bxy+2xz+2yz=4，可以经过正交变换=P化为椭圆柱面方程η2+4ζ2=4，求a,b的值和正交矩阵P.