设矩阵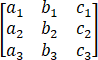 是满秩的,则直线(x-a3)/(a1-a2 )=(y-b3)/(b1-b2 )=(z-c3)/(c1-c2 )与直线(x-a1)/(a2-a3 )=(y-b1)/(b2-b3 )=(z-c1)/(c2-c3 )【 】
是满秩的,则直线(x-a3)/(a1-a2 )=(y-b3)/(b1-b2 )=(z-c3)/(c1-c2 )与直线(x-a1)/(a2-a3 )=(y-b1)/(b2-b3 )=(z-c1)/(c2-c3 )【 】
A、相交于一点
B、重合
C、平行但不重合
D、异面
设矩阵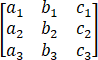 是满秩的,则直线(x-a3)/(a1-a2 )=(y-b3)/(b1-b2 )=(z-c3)/(c1-c2 )与直线(x-a1)/(a2-a3 )=(y-b1)/(b2-b3 )=(z-c1)/(c2-c3 )【 】
是满秩的,则直线(x-a3)/(a1-a2 )=(y-b3)/(b1-b2 )=(z-c3)/(c1-c2 )与直线(x-a1)/(a2-a3 )=(y-b1)/(b2-b3 )=(z-c1)/(c2-c3 )【 】
A、相交于一点
B、重合
C、平行但不重合
D、异面
A
已知α=(1,2,3);β=(1,1/2,1/3),设A=αTβ,则An=__________。
在上半平面求一条向上凹的曲线,其上任一点P(x,y)处的曲率等于此曲线在该点的法线段PQ长度的倒数(Q是法线与x轴的交点),且曲线在点(1,1)处的切线与x轴平行.
设向量组α1,α2,α3线性相关,α2,α3,α4线性无关,问:(1) α1能否由α2,α3线性表出?证明你的结论.(2) α4能否由α1,α2,α3线性表出?证明你的结论.
设直线l1:(x-1)/1=(y-5)/(-2)=(z+8)/1与l2:则l1与l2的夹角为【 】
已知点A与B的直角坐标分别为(1,0,0)与(0,1,1).线段AB绕z轴旋转一周所成的旋转曲面为S.求由S及两平面z=0,z=1所围成的立体体积.
设(a×b)∙c=2,则[(a+b)×(b+c)]∙(c+a)=________.
设空间直角坐标系中的四点A(1,1,1),B(1,2,3),C(1,2,4),D(2,3,4),则点A到平面BCD的距离d=__________.
设ξ,η是两个相互独立且均服从正态分布N(0,1/2)的随机变量,则随机变量|ξ-η|的数学期望E(|ξ-η|)=________.
设对任意x>0,曲线y=f(x)在点(x,f(x))处的切线在y轴上的截距等于1/x f(t)dt,求f(x)的一般表达式.
设B是秩为2的5×4矩阵,α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量,求Bx=0的解空间的一个标准正交基.
已知ξ=是矩阵A=的一个特征向量.(1)试确定参数a,b及特征向量ξ所对应的特征值;(2)问A能否相似于对角阵?说明理由.
甲乙两个盒子中各装有2个红球和2个白球,先从甲盒中任取一球,观察颜色后放入乙盒中,再从乙盒中任取一球.令X,Y分别表示从甲盒和乙盒中取到的红球个数,则X与Y的相关系数______.