已知函数f(x,y)=x³+y³-(x+y)²+3，设T是曲面z=f(x,y)在点(1,1,1)处的切平面，D为T与坐标平面所围成的有界区域在xOy平面上的投影.

(1)求T的方程；

(2)求f(x,y)在D上的最大值和最小值.

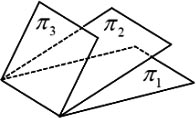
在空间直角坐标系O-xyz中，三张平面π_i:a_i x+b_i y+c_i z=d_i (i=1,2,3)的位置关系如图所示，记α_i=(a_i,b_i,c_i ),β_i=(a_i,b_i,c_i,d_i)，若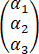r=m,r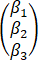=n，则【 】

A、m=1,n=2

B、m=n=2

C、m=2,n=3

D、m=n=3

证明双曲抛物面同族的任意两条直母线必是异面直线，且同族的全体直母线平行于同一个平面.

设函数f:R³→R,f(M)=Ax+By+Cz+D，其中A,B,C,D是不全为零的实数，M(x,y,z)∈R³.证明：如果三点M₀,M₁,M₂共线，且(M₁ M₀ ) ̅=λ(M₀ M₂ ) ̅,λ∈R,λ≠-1，那么

f(M₀ )=(f(M₁ )+λf(M₂))/(1+λ)

在直角坐标系下，已知一点M₀ (1,2,0)和一条直线L: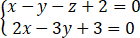，求M₀到L的距离，并写出过M₀且与L垂直相交的直线方程.