在空间直角坐标系O-xyz中,三张平面πi:ai x+bi y+ci z=di (i=1,2,3)的位置关系如图所示,记αi=(ai,bi,ci ),βi=(ai,bi,ci,di),若r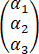 =m,r
=m,r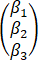 =n,则【 】
=n,则【 】
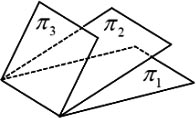
A、m=1,n=2
B、m=n=2
C、m=2,n=3
D、m=n=3
在空间直角坐标系O-xyz中,三张平面πi:ai x+bi y+ci z=di (i=1,2,3)的位置关系如图所示,记αi=(ai,bi,ci ),βi=(ai,bi,ci,di),若r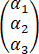 =m,r
=m,r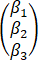 =n,则【 】
=n,则【 】

A、m=1,n=2
B、m=n=2
C、m=2,n=3
D、m=n=3
B
【解析】
解答过程见word版
设函数f(x)在区间(-1,1)上有定义,且f(x)=0,则【 】
已知幂级数anxn的和函数为ln(2+x),则na2n =【 】
设t>0,平面有界区域D由曲线y=√x ex与直线x=t,x=2t及x轴围成,D绕x轴旋转一周所成旋转体的体积为V(t),求V(t)的最大值.
设y(x)为微分方程x²y''+xy'-9y=0满足条件 y|x=1=2, y'|x=1=6的解.(1)利用变换x=et将上述方程化为常系数线性方程,并求y(x);(2)计算y(x)dx.
设平面有界区域D位于第一象限,由曲线xy=1/3,xy=3与直线y=1/3 x,y=3x围成,计算∬D(1+x-y)dxdy.
设向量α1=,α2=,α3=,若α1,α2,α3线性相关,且其中任意两个向量均线性无关,则ab=__________.
某物体以速度v(t)=t+ksinπt做直线运动,若它从t=0到t=3的时间段内平均速度是5/2,则k=__________.
设向量组α1,α2,α3线性相关,α2,α3,α4线性无关,问:(1) α1能否由α2,α3线性表出?证明你的结论.(2) α4能否由α1,α2,α3线性表出?证明你的结论.
已知α=(1,2,3);β=(1,1/2,1/3),设A=αTβ,则An=__________。
设函数f(x)在区间(-1,1)内有定义,且f(x)=0,则【 】
设函数f(x,y)在点(0,0)处可微,f(0,0)=0,n= (∂f/∂x,∂f/∂y,-1)|(0,0),非零向量r与n垂直,则【 】
设A,B,C为三个随机事件,且P(A)=P(B)=P(C)=1/4,P(AB)=0,P(AC)=P(BC)=1/12,则A,B,C中恰有一个事件发生的概率为【 】
在直角坐标系下,已知一点M0 (1,2,0)和一条直线L:,求M0到L的距离,并写出过M0且与L垂直相交的直线方程.
证明双曲抛物面同族的任意两条直母线必是异面直线,且同族的全体直母线平行于同一个平面.
计算R3中曲面(x12)/(a12 )+(x22)/(a22 )=(x32)/(a32 )与超平面x3=a3所围锥体的体积,a1,a2,a3>0.
设空间直角坐标系中的四点A(1,1,1),B(1,2,3),C(1,2,4),D(2,3,4),则点A到平面BCD的距离d=__________.
与两直线及(x+1)/1=(y+2)/2=(z-1)/1都平行且过原点的平面方程为______________.
过点M(1,2,-1)且与直线垂直的平面方程是__________.
已知两条直线的方程是 l1:(x-1)/1=(y-2)/0=(z-3)/(-1);l2:(x+2)/2=(y-1)/1=z/1.则过l1且平行于l2的平面方程是____________.
在上半平面求一条向上凹的曲线,其上任一点P(x,y)处的曲率等于此曲线在该点的法线段PQ长度的倒数(Q是法线与x轴的交点),且曲线在点(1,1)处的切线与x轴平行.