已知直线L1:(x-a2)/a1 =(y-b2)/b1 =(2-c2)/c1 与直线L2:(x-a3)/a2 =(y-b3)/b2 =(2-c3)/c2 相交与一点,法向量αi=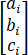 ,i=1,2,3,则【 】
,i=1,2,3,则【 】
A、α1可由a2,a3线性表示
B、α1可由a2,a3线性表示
C、α3可由a1,a2线性表示
D、α1,a2,a3线性无关
已知直线L1:(x-a2)/a1 =(y-b2)/b1 =(2-c2)/c1 与直线L2:(x-a3)/a2 =(y-b3)/b2 =(2-c3)/c2 相交与一点,法向量αi=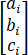 ,i=1,2,3,则【 】
,i=1,2,3,则【 】
A、α1可由a2,a3线性表示
B、α1可由a2,a3线性表示
C、α3可由a1,a2线性表示
D、α1,a2,a3线性无关
C
设函数f(x,y)在点(0,0)处可微,f(0,0)=0,n= (∂f/∂x,∂f/∂y,-1)|(0,0),非零向量r与n垂直,则【 】
设函数f(x)在区间(-1,1)内有定义,且f(x)=0,则【 】
设a1,a2,⋯,an是n个实数,都落在区间(-1,1)里.(1)证明 ∏1≤i,j≤n(1+aiaj)/(1-aiaj )≥1(2)找出以上不等式中等号成立的充分必要条件.
设f(a)=0,f(x)在[a,b]上的导数连续,求证:1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] |f'(x)|,x∈[a,b]
设α1=,α2=,α3=,α4=,若向量组α1,α2,α3与α1,α2,α4等价,则λ的取值范围是【 】
已知向量α1=,α2=,β1=,β2=,若γ既可由α1,α2线性表示,也可由β1,β2线性表示,则γ=【 】
已知向量α1=,α2=,α3=,β=,γ=k1 α1+k2 α2+k3 α3,若γTαi=βTαi (i=1,2,3),则k12+k22+k32=______.
向量组α1=(1 1 k),α2=(1 k 1),α3=(k 1 1)是线性无关的,则k=__________.
n维向量组α1,α2,…,αs (3≤s≤n)线性无关的充要条件是【 】
设A是n×n实对称矩阵,证明:存在一个实数k使得对任意一个实n维向量x都有|x' Ax|≤kx'x,其中x'表示向量x的转置.
设α1=,α2=,α3=,则三条直线a1 x+b1 y+c1=0,a2 x+b2 y+c2=0,a3 x+b3 y+c3=0,(其中ai2+bi2≠0,i=1,2,3)相交于一点的充要条件是【 】
设B是秩为2的5×4矩阵,α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量,求Bx=0的解空间的一个标准正交基.
设A是n阶矩阵,若存在正整数k,使线性方程组Akx=0有解向量α,且Ak-1α≠0,证明向量组α,Aα,…,Ak-1α是线性无关的.
设R^3上的线性变换A(x)=x,则α=生成的A-循环不变空间的维数为________.
设A是n阶复方阵,V1是A的行向量生成的Cn的子空间,V2是A的列向量生成的Cn的子空间,则V1=V2.
设α1,α2,…,αr是n维向量.令β1=α2+α3+⋯+αr,β2=α1+α3+⋯+αr,…,βr=α1+α2+⋯+αr-1.证明向量组β1,β2,…,βr与向量组α1,α2,…,αr有相同的秩.