大学数学-考研试题(重庆大学 2004年向量空间)

填空题（2004年重庆大学）

设R²中的内积为(α,β)=α' Aβ,A=，则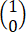,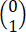在此内积之下的度量矩阵为________.

答案解析

暂无答案

讨论

大学数学

若A=相似于对角阵，则a与b的关系为________.

若不可约多项式p(x)是f(k)(x)的s重因子，且p(x)|f(x)，那么p(x)________ f(x)的s+k重因子.

三阶方阵A的特征值为1,-1,2，则A2+4A-1的特征值=________.

设γ1,γ2,α,β皆为三维列向量，A=(α,3γ1,3γ2 ),B=(β,γ1,2γ2)且|A|=18,|B|=4，则|A-B|=________.

三阶行列式有2个元素为4，其余为±1，则此行列式可能的最大值为________.

已知矩阵：A=,B=,C= 计算：(cosα∙A+cosβ∙B+cosγ∙C)3=？其中，cos2 α+cos2 β+cos2 γ=1,cosα+2cosβ+3cosγ=√3/3.提示：设E=，并引入三个矩阵：A'=A-E,B'=B-2E,C'=C-3E [注意：(cosα∙A'+cosβ∙B'+cosγ∙C')2=？]后，再作计算.

已知四维实矢量空间的矢量（表示成矩阵）：=,满足如下条件：以及T∙=9/4（其中，T表示对矩阵取置换），试求出所有这样的四维实矢量的集合：{ }=?

由曲线y=y(x)=(-√3<x≤0)和射线y=-√3 x(x≤0)，以及由曲线y=y(x)=(-√3<x≤0)和射线y=-√3 x(x≤0)，直线x=-√3围成了两块平面图形F1和F2（其中，F1的边界长度为有限值，而F2的边界长度为无穷大）.(1)计算出平面图形F1的面积S1=？(2)计算出平面图形F2的面积S2=？提示：采用平面极坐标(r,θ)作计算较为简单.[不定积分公式：∫tg2θdθ=tgθ-θ+C可直接引用]

设曲面：z=z(x,y)=x4+1/2 (√5-4y)∙x2+y2，柱壁面：y=x2-5/9，圆柱体：x2+y2≤1，在三维空间O-XYZ中的“点的集合”分别为G1,G2,G3.(1)说明“点集”：G=G1∩G2∩G3构成了在三维空间O-XYZ中的有限长度的曲线L.(2)采用“参数方程”：，[t∈T；(T为参变数t的“取值集合”)]表示出曲线L.(3)计算曲线L的“总长度”：L=？提示：(i)选择参变数t=x,(ii)考虑柱壁面：y=x2-5/9与圆柱面：x2+y2=1满足相交或满足相切？[不定积分公式：∫dx=x/2 +a2/2 ln⁡(x+)+C可直接引用]

已知一个二元实变函数：z=f(x,y)=sin2x - sinx∙cosy+cos2y;[其中，(x,y)∈全平面].(1)求出函数z=f(x,y)在其定义域里的最小值：zmin=？并指出在其定义域何点处，函数z=f(x,y)获得最小值zmin？(2)求出函数z=f(x,y)在其定义域里的最大值：zmax=？并指出在其定义域何点处，函数z=f(x,y)取得最大值zmax？提示：首先，可作变量变换：X=sinx,Y=cosy；然后，考虑关于X和Y的二元实变函数z=F(X,Y).

向量空间

设A=(aij)n×n是一个由±1组成的n×n方阵(n>1).将A的n个行向量记为v1,…,vn.对于两个行行向量v=(ai)1≤i≤n与v'=(bi)1≤i≤n，定义v*v'=(aibi)1≤i≤n以及v∙v'=aibi假设：(1)对任意的i,j(1≤i,j≤n)，存在k(1≤k≤n)使得vi*vj=vk；(2)对任意的i,j(1≤i,j≤n,i≠j)， vi∙vj=0.证明：(i) A有一个行向量；对于A的另外任意一个行向量v_i，它有n/2个分量为1，n/2个分量为-1.(ii)n是2的幂.(ii)设n=2m，则可以通过重新排列A的行与列，将A变为方阵这里，X⨂m==是方阵X的m次张量积：两个方阵X=(xij)1≤i,j≤p与Y=(yi'j')1≤i',j'≤q的张量积被定义为一个pq×pq方阵X⨂Y=(zkl)1≤kl≤pq其中zkl=xijyi'j'，整数i,j,i',j'满足1≤i,j≤p,1≤i',j'<q，且由等式k=p(i'-1)+i与l=p(j'-1)+j唯一确定.

设对角矩阵A的特征多项式为 φ(λ)=(λ-λi)ni （诸λi两两互异），求所有和A可交换的矩阵全体所组成的线性空间的维数.

用数学归纳法证明：对于复n维空间Vn上任意多个两两可交换的线性变换所组成的集合S具有公共的特征向量.

设α1=(1,0,0,3),α2=(1,1,-1,2),α3=(1,2,a-3,1),α4=(1,2,-2,a),β=(0,1,b,-1)，问a,b为何值时(1) β能由α1,α2,α3,α4线性表示且表示唯一；(2) β不能由α1,α2,α3,α4线性表示；(3) β能由α1,α2,α3,α4线性表示但表示不唯一，并求一般表达式。

已知全体实的2维向量关于下列运算构成R上的线性空间V：(a1,b1 )+(a2,b2 )=(a1+a2,b1+b2+a1 a2),k∙(a,b)=(ka,kb+(k(k-1))/2 a2).(1)求V的一组基;(2)定义变换A(a,b)=(a,a+b)，证明：A是一个线性变换；并求A在V的一组基下的矩阵表示.

设A是n维线性空间V的线性变换，则V=ImA⊕KerA.

已知A ̅和B ̅分别是三维空间中的矢量矩阵和单位方向矢量;A ̅=Ax+Ay+Az;( Ax=,Ay=,Az=B ̅=cosα+cosβ+cosγ;( cos2 α+cos2 β+cos2 γ=1)计算矩阵求和c=k(A ̅∙B ̅)k +2k (A ̅∙B ̅)2k.提示：首先考察(A ̅∙B ̅)2=?

在P[x]4定义内积：(f(x),g(x))=f(x)g(x) dx,f(x),g(x)∈P[x]4，并定义线性变换A:Aεi=ηi,i=1,2,3,4.ε1=1/2 (1+x+x2+x3 ),η1=2x+x2-x3 ε2=1/2 (-1-x+x2+x3 ),η2=-1-x2-2x3 ε3=1/2 (-1+x-x2+x3 ),η3=-2x-x2+x3 ε4=1/2 (-1+x+x2-x3 ),η4=1-4x-x2 求A的核空间的一个标准正交基.

设B是秩为2的5×4矩阵，α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量，求Bx=0的解空间的一个标准正交基.

设R^3上的线性变换A(x)=x，则α=生成的A-循环不变空间的维数为________.

向量组的线性相关性

设α1,α2,…,αr是n维向量.令β1=α2+α3+⋯+αr,β2=α1+α3+⋯+αr,…,βr=α1+α2+⋯+αr-1.证明向量组β1,β2,…,βr与向量组α1,α2,…,αr有相同的秩.

设A是n×n实对称矩阵，证明：存在一个实数k使得对任意一个实n维向量x都有|x' Ax|≤kx'x，其中x'表示向量x的转置.

四维矢量X采用列矩阵表示为：X=,其中，矢量X的四个分量x1,x2,x3,x4满足如下条件：，试证明：这样的四维矢量X存在“无穷多个”，并可一般表示为：X=ax1+bx2+1/2 x3;其中x1=,x2=,x3=;而a,b为“任意实数”.

设α1=,α2=,α3=，则三条直线a1 x+b1 y+c1=0,a2 x+b2 y+c2=0,a3 x+b3 y+c3=0,(其中ai2+bi2≠0,i=1,2,3)相交于一点的充要条件是【】

设A是n阶复方阵，V1是A的行向量生成的Cn的子空间，V2是A的列向量生成的Cn的子空间，则V1=V2.

已知向量α1=,α2=,α3=,β=,γ=k1 α1+k2 α2+k3 α3，若γTαi=βTαi (i=1,2,3)，则k12+k22+k32=______.

设向量组A:α1,α2,… ,αs可以由向量组B:β1,β2,… ,βt线性表示且R(A)=R(B).证明向量组A与向量组B等价.

设A是n×m矩阵，B是m×n矩阵，其中n<m，E是n阶单位矩阵，若AB=E，证明B的列向量组线性无关.

设α1=,α2=,α3=,α4=，若向量组α1,α2,α3与α1,α2,α4等价，则λ的取值范围是【】

已知同维数的两个向量组有相同的秩，且其中之一可用另外一个线性表示，证明：这两个向量组等价。