在P[x]4定义内积:(f(x),g(x))=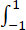 f(x)g(x) dx,f(x),g(x)∈P[x]4,并定义线性变换A:Aεi=ηi,i=1,2,3,4.
f(x)g(x) dx,f(x),g(x)∈P[x]4,并定义线性变换A:Aεi=ηi,i=1,2,3,4.
ε1=1/2 (1+x+x2+x3 ),η1=2x+x2-x3
ε2=1/2 (-1-x+x2+x3 ),η2=-1-x2-2x3
ε3=1/2 (-1+x-x2+x3 ),η3=-2x-x2+x3
ε4=1/2 (-1+x+x2-x3 ),η4=1-4x-x2
求A的核空间的一个标准正交基.
在P[x]4定义内积:(f(x),g(x))=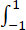 f(x)g(x) dx,f(x),g(x)∈P[x]4,并定义线性变换A:Aεi=ηi,i=1,2,3,4.
f(x)g(x) dx,f(x),g(x)∈P[x]4,并定义线性变换A:Aεi=ηi,i=1,2,3,4.
ε1=1/2 (1+x+x2+x3 ),η1=2x+x2-x3
ε2=1/2 (-1-x+x2+x3 ),η2=-1-x2-2x3
ε3=1/2 (-1+x-x2+x3 ),η3=-2x-x2+x3
ε4=1/2 (-1+x+x2-x3 ),η4=1-4x-x2
求A的核空间的一个标准正交基.
暂无答案
设α1,α2,…,αr是n维向量.令β1=α2+α3+⋯+αr,β2=α1+α3+⋯+αr,…,βr=α1+α2+⋯+αr-1.证明向量组β1,β2,…,βr与向量组α1,α2,…,αr有相同的秩.
设A是n×n实对称矩阵,证明:存在一个实数k使得对任意一个实n维向量x都有|x' Ax|≤kx'x,其中x'表示向量x的转置.
向量组α1=(1 1 k),α2=(1 k 1),α3=(k 1 1)是线性无关的,则k=__________.
已知四维实矢量空间的矢量(表示成矩阵):=,满足如下条件:以及T∙=9/4(其中,T表示对矩阵取置换),试求出所有这样的四维实矢量的集合:{ }=?
已知同维数的两个向量组有相同的秩,且其中之一可用另外一个线性表示,证明:这两个向量组等价。
设B是秩为2的5×4矩阵,α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量,求Bx=0的解空间的一个标准正交基.
设α1=,α2=,α3=,α4=,若向量组α1,α2,α3与α1,α2,α4等价,则λ的取值范围是【 】
已知向量α1=,α2=,α3=,β=,γ=k1 α1+k2 α2+k3 α3,若γTαi=βTαi (i=1,2,3),则k12+k22+k32=______.