大学数学-考研试题(中国科学技术大学 2022年向量空间)

填空题（2022年中国科学技术大学）

设R^3上的线性变换A(x)=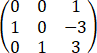x，则α=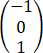生成的A-循环不变空间的维数为________.

答案解析

暂无答案

讨论

大学数学

设=QR，其中Q是正交方阵，R是对角线元素大于0的上三角方阵，则R=________.

设A=，则A-1=__________，A2022=__________，A的最大奇异值σ1=__________.

设空间直角坐标系中的四点A(1,1,1),B(1,2,3),C(1,2,4),D(2,3,4),则点A到平面BCD的距离d=__________.

在平面直角坐标系中，椭圆x2+xy+y2=1的长轴方程为__________，位于x轴上半平面内的焦点坐标为__________.

设f(x)=sin⁡(a1 x)+sin⁡(a2 x)+sin⁡(a3 x),a1,a2,a3>0.证明：存在数列{tn}使得tn=+∞且f(x+tn)=f(x)对∀x∈R一致成立.

设函数f:R→R在R/{x0}上有二阶导数，满足：当x∈(-∞,x0)时f' (x)<0<f''(x)，而当x∈(x0,+∞)时，f' (x)>0>f''(x)，证明：f在x0处不可微.

设函数f:R→R满足：(1) f(1)=1,(2) f'(x)=1/(x2+[f(x)]2),∀x≥1.证明：f(x)存在且小于1+π/4.

设f:[0,1]→[0,1]是一个连续函数，证明：方程2x-f(t)dt=1在[0,1]中有且仅有一个零点.

试问函数f(x,y)=sin⁡[π/(1-x2-y2 )]在区域D:{(x,y)∈R2;x2+y2<1}上是否一致连续？证明你的结论.

设u(x,y,z)=，证明：d2u≥0.

向量空间

设对角矩阵A的特征多项式为 φ(λ)=(λ-λi)ni （诸λi两两互异），求所有和A可交换的矩阵全体所组成的线性空间的维数.

用数学归纳法证明：对于复n维空间Vn上任意多个两两可交换的线性变换所组成的集合S具有公共的特征向量.

设R2中的内积为(α,β)=α' Aβ,A=，则,在此内积之下的度量矩阵为________.

已知全体实的2维向量关于下列运算构成R上的线性空间V：(a1,b1 )+(a2,b2 )=(a1+a2,b1+b2+a1 a2),k∙(a,b)=(ka,kb+(k(k-1))/2 a2).(1)求V的一组基;(2)定义变换A(a,b)=(a,a+b)，证明：A是一个线性变换；并求A在V的一组基下的矩阵表示.

已知A ̅和B ̅分别是三维空间中的矢量矩阵和单位方向矢量;A ̅=Ax+Ay+Az;( Ax=,Ay=,Az=B ̅=cosα+cosβ+cosγ;( cos2 α+cos2 β+cos2 γ=1)计算矩阵求和c=k(A ̅∙B ̅)k +2k (A ̅∙B ̅)2k.提示：首先考察(A ̅∙B ̅)2=?

在P[x]4定义内积：(f(x),g(x))=f(x)g(x) dx,f(x),g(x)∈P[x]4，并定义线性变换A:Aεi=ηi,i=1,2,3,4.ε1=1/2 (1+x+x2+x3 ),η1=2x+x2-x3 ε2=1/2 (-1-x+x2+x3 ),η2=-1-x2-2x3 ε3=1/2 (-1+x-x2+x3 ),η3=-2x-x2+x3 ε4=1/2 (-1+x+x2-x3 ),η4=1-4x-x2 求A的核空间的一个标准正交基.

设B是秩为2的5×4矩阵，α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量，求Bx=0的解空间的一个标准正交基.

设A=(aij)n×n是一个由±1组成的n×n方阵(n>1).将A的n个行向量记为v1,…,vn.对于两个行行向量v=(ai)1≤i≤n与v'=(bi)1≤i≤n，定义v*v'=(aibi)1≤i≤n以及v∙v'=aibi假设：(1)对任意的i,j(1≤i,j≤n)，存在k(1≤k≤n)使得vi*vj=vk；(2)对任意的i,j(1≤i,j≤n,i≠j)， vi∙vj=0.证明：(i) A有一个行向量；对于A的另外任意一个行向量v_i，它有n/2个分量为1，n/2个分量为-1.(ii)n是2的幂.(ii)设n=2m，则可以通过重新排列A的行与列，将A变为方阵这里，X⨂m==是方阵X的m次张量积：两个方阵X=(xij)1≤i,j≤p与Y=(yi'j')1≤i',j'≤q的张量积被定义为一个pq×pq方阵X⨂Y=(zkl)1≤kl≤pq其中zkl=xijyi'j'，整数i,j,i',j'满足1≤i,j≤p,1≤i',j'<q，且由等式k=p(i'-1)+i与l=p(j'-1)+j唯一确定.

设α1=(1,0,0,3),α2=(1,1,-1,2),α3=(1,2,a-3,1),α4=(1,2,-2,a),β=(0,1,b,-1)，问a,b为何值时(1) β能由α1,α2,α3,α4线性表示且表示唯一；(2) β不能由α1,α2,α3,α4线性表示；(3) β能由α1,α2,α3,α4线性表示但表示不唯一，并求一般表达式。

已知三维向量空间的基底为α1=(1,1,0)T,α2=(1,0,1)T,α3=(0,1,1)T，则向量β=(2,0,0)T在此基底下的坐标是____________.

向量组的线性相关性

设α1,α2,…,αr是n维向量.令β1=α2+α3+⋯+αr,β2=α1+α3+⋯+αr,…,βr=α1+α2+⋯+αr-1.证明向量组β1,β2,…,βr与向量组α1,α2,…,αr有相同的秩.

已知同维数的两个向量组有相同的秩，且其中之一可用另外一个线性表示，证明：这两个向量组等价。

设向量组A:α1,α2,… ,αs可以由向量组B:β1,β2,… ,βt线性表示且R(A)=R(B).证明向量组A与向量组B等价.

设xoy在平面上n个结点Mi(xi,yi ),i=1,2,…,n(n≥3).证明：M1,M2,…,Mn在同一条直线上⟺R=2.

已知向量组α1=(1,2,3,4),α2=(2,3,4,5),α3=(3,4,5,6),α4=(4,5,6,7)，则该向量组的秩是______.

设α1=,α2=,α3=，则三条直线a1 x+b1 y+c1=0,a2 x+b2 y+c2=0,a3 x+b3 y+c3=0,(其中ai2+bi2≠0,i=1,2,3)相交于一点的充要条件是【】

设A是n阶矩阵，若存在正整数k，使线性方程组Akx=0有解向量α，且Ak-1α≠0，证明向量组α,Aα,…,Ak-1α是线性无关的.

已知α1=(1,0,2,3),α2=(1,1,3,5),α3=(1,-1,a+2,1),α4=(1,2,4,a+8)及β=(1,1,b+3,5).(1) a,b为何值时，β不能表示成α1,α2,α3,α4的线性组合？(2) a,b为何值时，β有α1,α2,α3,α4的唯一线性表示？并写出该表示式.

设A是n×m矩阵，B是m×n矩阵，其中n<m，E是n阶单位矩阵，若AB=E，证明B的列向量组线性无关.

已知向量组α1,α2,α3,α4线性无关，则向量组【】