设u(x,y,z)=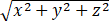
，证明：d2u≥0.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设u=f(x,y,z),φ(x2,ey,z)=0,y=sinx，其中f,φ都具有一阶连续偏导数，且∂φ/∂z≠0,求du/dx.
函数u=ln(x+)在A(1,0,1)处沿A点指向B(3,-2,2)点方向的方向导数为________.
设直线l:在平面π上，且平面π与曲面z=x2+y2相切于点(1,-2,5)，求a,b的值.
设函数f(u)具有二阶连续导数，而z=f(exsiny)满足方程∂2z/∂x2+∂2z/∂y2=e2x z,求f(u).
设z=1/x f(xy)+yφ(x+y),f,φ具有二阶连续导数，则∂2z/∂x∂y=________________.
设y=y(x),z=z(x)是由方程z=xf(x+y)和F(x,y,z)=0所确定的函数，其中f和F分别具有一阶连续导数和一阶连续偏导数，求dz/dx.
函数f(x,y)=x2+2y2在(0,1)的最大方向导数为______.
设f,g为连续可微函数，u=f(x,xy),v=g(x+xy)，求∂u/∂x∙∂v/∂x
设u=yf(x/y)+xg(y/x)，其中函数f,g具有二阶连续导数，求x ∂2u/∂x2+y ∂2u/∂x∂y .
设z=f(2x-y)+g(x,xy)，其中函数f(t)二阶可导，g(u,v)具有连续的二阶偏导数，求∂2z/∂x∂y.
设z=f(2x-y,ysinx)，其中f(u,v)具有连续的二阶偏导数，求∂2z/∂x∂y.
设z=f(ex siny,x2+y2)，其中f具有二阶连续偏导数，求∂2z/∂x∂y.
设函数f:R→R在R/{x0}上有二阶导数，满足：当x∈(-∞,x0)时f' (x)<0<f''(x)，而当x∈(x0,+∞)时，f' (x)>0>f''(x)，证明：f在x0处不可微.
设A=，则A-1=__________，A2022=__________，A的最大奇异值σ1=__________.