设y=y(x),z=z(x)是由方程z=xf(x+y)和F(x,y,z)=0所确定的函数，其中f和F分别具有一阶连续导数和一阶连续偏导数，求dz/dx.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（1999年理工数学Ⅰ）
答案解析
分别在z=xf(x+y)和F(x,y,z)=0的两边对x求导，得
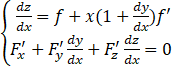，整理后得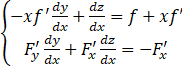
,
解得dz/dx=((f+xf') Fy'-xf'Fz')/(Fy'+xf'Fz' ),其中Fy'+xf'Fz'≠0.
讨论
已知((x+ay)dx+ydy)/(x+y)2 为某函数的全微分，则a等于【 】
若f(x,y)在区域D内对x和y都是连续的，则f(x,y)对(x,y)D为二元连续.
求函数f(x,y)=1/2(xn+yn)（n是正整数）在条件x+y=a（x≥0,y≥0，常数a>0）下的极值.
设参数方程x=f'(t),y=tf'(t)-f(t)，其中函数f(t)可以求导足够次数，求一阶导数dy/dx和二阶导数d2y/dx2.
设f,g为连续可微函数，u=f(x,xy),v=g(x+xy)，求∂u/∂x∙∂v/∂x
设u=yf(x/y)+xg(y/x)，其中函数f,g具有二阶连续导数，求x ∂2u/∂x2+y ∂2u/∂x∂y .
已知曲面z=4-x2-y2上点P处的切平面平行于平面2x+2y+z-1=0，则点P的坐标是【 】
设u=f(x,y,z),φ(x2,ey,z)=0,y=sinx，其中f,φ都具有一阶连续偏导数，且∂φ/∂z≠0,求du/dx.
设x(y),z(y)是由方程组所确定的隐函数，求x'(y),z'(y).
设u=u(x,y),v=v(x,y)由方程所确定，求∂u/∂x,∂v/∂x.
在区间(0,2)上随机取一点，将该区间分成两段，较短的一段长度记为X，较长的一段记为Y，令Z=Y/X.(1) 求X的概率密度；(2) 求Z的概率密度；(3) 求E(X/Y).
已知连续随机变量X的概率密度函数为f(x)=，则X的数学期望为______；X的方差为______.
设随机变量X服从均值为10，均方差为0.02的正态分布，已知Φ(x)=du, Φ(2.5)=0.9938,则X落在区间(9.95,10.05)内的概率为______.
设随机变量X的概率密度函数为fX(x)=1/(π(1+x2))，求随机变量Y=1-∛X的概率密度函数fY(y).