已知连续随机变量X的概率密度函数为f(x)=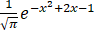
，则X的数学期望为______；X的方差为______.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
随机变量z ~ N(2,32)，则y=3z-2的数学期望为【 】
某车站于每个钟点的第5分钟、25分钟、50分钟发出一班车。假设一个乘客在某个钟点的第X分钟到达车站，且X在[0,60]上均匀分布。请计算该乘客的平均等候时间。
随机变量X密度函数为f(x)=试求：(1)A值 (2)X的分布函数F(x) (3) E=(1/X2 ) (4) D(X)
设随机变量X服从参数为1的泊松分布，则E(|X-EX|)=【 】
设ξ,η是两个相互独立且均服从正态分布N(0,1/2)的随机变量，则随机变量|ξ-η|的数学期望E(|ξ-η|)=________.
设随机变量X服从参数为1的指数分布，则数学期望E(X+e-2X )=__________.
从学校乘汽车到火车站的途中有3个交通岗，假设在各交通岗遇到红灯的事件是相互独立的，并且概率都是2/5.设X为途中遇到红灯的次数，求随机变量X的分布律、分布函数和数学期望.
设X表示10次独立重复射击命中目标的次数，每次射中目标的概率为0.4，则X2的数学期望E(X2)=________.
已知离散型随机变量X服从参数为2的泊松分布，即P{X=k}=2ke-2/k!,k=0,1,2,…，则随机变量Z=3X-2的期望E(Z)=________.
设两个相互独立的随机变量X和Y的方差分别为4和2，则随机变量3X-2Y的方差是【 】
设二维随机变量(X,Y)的概率密度为f(x,y)=(Ⅰ)求X与Y的方差；(Ⅱ)X与Y是否相互独立；(Ⅲ)求Z=X²+Y²的概率密度.
设随机变量X~N(0,4)，随机变量Y~B(3 ,1/3)，且X与Y不相关，则D(X-3Y+1)=【 】
与两直线及(x+1)/1=(y+2)/2=(z-1)/1都平行且过原点的平面方程为______________.
设L为取正向的圆周x2+y2=9，则曲线积分∮L(2xy-2y)dx+(x2 - 4x)dy=________.
已知三维向量空间的基底为α1=(1,1,0)T,α2=(1,0,1)T,α3=(0,1,1)T，则向量β=(2,0,0)T在此基底下的坐标是____________.
设两个相互独立的随机变量X和Y分别服从正态分布N(0,1)和N(1,1)，则【 】
设随机变量X~N(0,1)，在X=x条件下，随机变量Y~N(x,1)，则X与Y的相关系数为【 】
(X,Y)的联合概率分布为试求：(1)DX (2)DY (3)cov(X,Y)
设二维随机变量(X,Y)的概率分布为X\Y 0 1 2-1 0.1 0.1 b1 a 0.1 0.1若事件{max(X,Y)=2}与事件{min(X,Y)=1}相互独立，则Cov(X,Y)=【 】
设随机变量X服从(0,2)上的均匀分布，则随机变量Y=X2在(0,4)内的概率分布密度fY(y)=__________.
设随机变量X服从均值为10，均方差为0.02的正态分布，已知Φ(x)=du, Φ(2.5)=0.9938,则X落在区间(9.95,10.05)内的概率为______.
设直线l:在平面π上，且平面π与曲面z=x2+y2相切于点(1,-2,5)，求a,b的值.
设函数f(u)具有二阶连续导数，而z=f(exsiny)满足方程∂2z/∂x2+∂2z/∂y2=e2x z,求f(u).