-
关注“优题吧”，分配平台账号.
竞赛2024年阿里巴巴( )
小明玩战机游戏. 初始积分为2. 在游戏进行中，积分会随着时间线性地连续减少（速率为每单位时间段扣除1）。游戏开始后，每隔一个随机时间段（时长为互相独立的参数为1的指数分布)，就会有一架敌机出现在屏幕上。当敌机出现时，小明立即进行操作，可以瞬间击落对方，或者瞬间被对方击落。如被敌机击落，则游戏结束。如小明击落敌机，则会获得1.5个积分，并且可以选择在击落该次敌机后立即退出游戏，或者继续游戏。如选择继续游戏，则须等待到下一架敌机出现，中途不能主动退出。游戏的难度不断递增：出现的第n架敌机，小明击落对方的概率为(0.85)n，被击落的概率为1-(0.85)n，且与之前的事件独立。在任何时刻，如果积分降到0，则游戏自动结束。
问题部分：
(1) 如果游戏中，小明被击落后，其之前的积分保持。那么为了游戏结束时的累积积分的数学期望最大化，小明应该在其击落第几架敌机后主动结束游戏?
(A)1 (B)2 (C)3 (D)4
(2) 假设游戏中，小明被击落后，其之前积累的积分会清零。那么为了结束时的期望积分最大化，小明也会选择一个最优的时间主动结束游戏。请问在游戏结束时(小明主动结束、或积分减到0)，下列哪一个选项最接近游戏结束时小明的期望积分?
(A)2 (B)4 (C)6 (D)8
(1)B (2)A
解答过程见word版.
考研2024年经济数学Ⅲ( )
设随机变量X的概率密度为f(x)=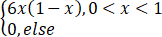
，则X的三阶中心矩E(X-EX)³=【 】
A、-1/32
B、0
C、1/16
D、1/2
解答过程见word版
考研2024年理工数学Ⅰ( )
设随机变量X的概率密度为f(x)=
，在X=x(0<x<1)的条件下，随机变量Y服从区间(x,1)上的均匀分布，则Cov(X,Y)=【 】
A、-1/36
B、-1/72
C、1/72
D、1/36
解答过程见word版
考研2020年理工数学Ⅰ( )
设X服从区间(-π/2,π/2)的均匀分布，Y=sinX，则Cov(X,Y)=________.
2/π
详细过程见word版
考研2023年理工数学Ⅰ( )
设二维随机变量(X,Y)的概率密度为
f(x,y)=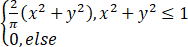
(Ⅰ)求X与Y的方差；
(Ⅱ)X与Y是否相互独立；
(Ⅲ)求Z=X²+Y²的概率密度.
(Ⅰ) E(X)=∬Dx 2/π(x2+y2)dσ=0;
E(X2 )=∬Dx2 2/π(x2+y2) dσ=4∬D1x2 2/π(x2+y2)dσ
=4/π ∬D1(x2+y2 )2 dσ=4/π 
dθ 
r5dr=1/3
所以D(X)=1/3，同理D(Y)=1/3.
(Ⅱ) fX (x)=
=
同理得：fY (x)=
因为fX (x) fY (y)≠f(x,y)，所以X与Y不相互独立.
(Ⅲ) FZ (z)=P(Z≤z)=P{X2+Y2≤z}
当z<0时，FZ (z)=0；
当0≤z<1时，FZ (z)=∬Dz2/π(x2+y2)dσ=2/π 
dθ 
r3 dr=z2;
当z≥1时，FZ (z)=1;
所以，Z的概率密度为fZ (z)=
.