设随机变量X的概率密度为f(x)=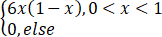
，则X的三阶中心矩E(X-EX)³=【 】
A、-1/32
B、0
C、1/16
D、1/2
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设X服从区间(-π/2,π/2)的均匀分布，Y=sinX，则Cov(X,Y)=________.
设随机变量X的概率密度为f(x)=，在X=x(0<x<1)的条件下，随机变量Y服从区间(x,1)上的均匀分布，则Cov(X,Y)=【 】
某种原材料一天的消耗量是一个随机变量，概率密度函数为f(x)=，设每天的消耗量是相互独立的，分别求：两天的消耗量X和三天的消耗量Y的概率密度函数。
设随机变量X,Y相互独立，其概率密度函数分别为：fX (x)=,fY(y)= 求Z=2X+Y的概率密度函数.
设随机变量X与Y独立，且X服从均值为1、标准差（均方差）为√2的正态分布，而Y服从标准正态分布，试求随机变量Z=2X-Y+3的概率密度函数.
已知随机变量X的概率密度函数f(x)=1/2 e-|x|,-∞<x<+∞，则X的概率分布函数F(x)=____________.
设随机变量X与Y独立，X服从正态分布N(μ,σ2)，Y服从[-π,π]上的均匀分布，试求Z=X+Y的概率分布密度（计算结果用标准正态分布函数Φ(x)表示，其中Φ(x)=dt）.
设随机变量X1,X2,…,Xn独立同分布，且X1的4阶矩阵存在.设μk=E(X1k)(k=1,2,3,4)，则由切比雪夫不等式，对∀ε>0，有P{|1/n Xi2 -μ2 |≥ϵ}≤【 】
设二维随机变量(X,Y)的概率分布为X\Y 0 1 2-1 0.1 0.1 b1 a 0.1 0.1若事件{max(X,Y)=2}与事件{min(X,Y)=1}相互独立，则Cov(X,Y)=【 】
设函数f(x)=(1+x)/(1+nx2n)，则f(x)【 】
设二次型f(x1,x2,x3 )=xT Ax在正交变换下可化成y1²-2y2²+3y3²，则二次型f的矩阵A的行列式值与迹分别为【 】
设矩阵A=,Mij表示A的i行j列元素的余子式.若|A|=-1/2，且-M21+M22-M23=0，则【 】
随机变量X,Y相互独立，其X~N(0,2),Y~N(-1,1)，记p1={2X>Y},p2={X-2Y>1}，则【 】
已知连续随机变量X的概率密度函数为f(x)=，则X的数学期望为______；X的方差为______.
设随机变量X服从均值为10，均方差为0.02的正态分布，已知Φ(x)=du, Φ(2.5)=0.9938,则X落在区间(9.95,10.05)内的概率为______.
已知离散型随机变量X服从参数为2的泊松分布，即P{X=k}=2ke-2/k!,k=0,1,2,…，则随机变量Z=3X-2的期望E(Z)=________.
设随机变量X服从参数为1的指数分布，则数学期望E(X+e-2X )=__________.
设随机变量X服从(0,2)上的均匀分布，则随机变量Y=X2在(0,4)内的概率分布密度fY(y)=__________.
设X表示10次独立重复射击命中目标的次数，每次射中目标的概率为0.4，则X2的数学期望E(X2)=________.
设ξ,η是两个相互独立且均服从正态分布N(0,1/2)的随机变量，则随机变量|ξ-η|的数学期望E(|ξ-η|)=________.