设随机变量X与Y独立,X服从正态分布N(μ,σ2),Y服从[-π,π]上的均匀分布,试求Z=X+Y的概率分布密度(计算结果用标准正态分布函数Φ(x)表示,其中Φ(x)=
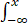
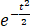 dt).
dt).
问答题(1992年理工数学Ⅰ)
答案解析
由题设知X与Y的概率密度分别为fX (x)=,-∞<x<+∞,fY (y)=,由卷积公式知Z的概率密度为fZ (z)=〖fX (x-y) fY (y)〗 dy=dy,令t=(z-y-μ)/...
查看完整答案讨论
设随机变量X与Y独立,且X服从均值为1、标准差(均方差)为√2的正态分布,而Y服从标准正态分布,试求随机变量Z=2X-Y+3的概率密度函数.
已知随机变量X的概率密度函数f(x)=1/2 e-|x|,-∞<x<+∞,则X的概率分布函数F(x)=____________.
设二维随机变量(X,Y)在区域D:0<x<1,|y|<x内服从均匀分布,求关于X的边缘概率密度函数及随机变量Z=2X+1的方差D(Z).
若随机变量X服从均值为2、方差为σ2的正态分布,且P{2<X<4}=0.3,则P{X<0}=________.
甲乙两个盒子中各装有2个红球和2个白球,先从甲盒中任取一球,观察颜色后放入乙盒中,再从乙盒中任取一球.令X,Y分别表示从甲盒和乙盒中取到的红球个数,则X与Y的相关系数______.
在区间(0,2)上随机取一点,将该区间分成两段,较短的一段长度记为X,较长的一段记为Y,令Z=Y/X.(1) 求X的概率密度;(2) 求Z的概率密度;(3) 求E(X/Y).
设二维随机变量(X,Y)的概率密度为f(x,y)=,求随机变量Z=X+2Y的分布函数.
某车站于每个钟点的第5分钟、25分钟、50分钟发出一班车。假设一个乘客在某个钟点的第X分钟到达车站,且X在[0,60]上均匀分布。请计算该乘客的平均等候时间。
某种原材料一天的消耗量是一个随机变量,概率密度函数为f(x)=,设每天的消耗量是相互独立的,分别求:两天的消耗量X和三天的消耗量Y的概率密度函数。
设随机变量X,Y相互独立,其概率密度函数分别为:fX (x)=,fY(y)= 求Z=2X+Y的概率密度函数.
设随机变量X1,X2,…,Xn独立同分布,且X1的4阶矩阵存在.设μk=E(X1k)(k=1,2,3,4),则由切比雪夫不等式,对∀ε>0,有P{|1/n Xi2 -μ2 |≥ϵ}≤【 】
设平面区域D由曲线y=1/x及直线y=0,x=1,x=e2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)关于X的边缘概率密度在x=2处的值为________.
设两个随机变量X、Y相互独立,且都服从均值为0、方差为1/2的正态分布,求随机变量|X-Y|的方差.
设X和Y为两个随机变量,且P{X≥0,Y≥0}=3/7,P{X≥0}=P{Y≥0}=4/7,则P{max(X,Y)≥0}=________.
相互独立的两个随机变量X,Y具有同一分布律,且X的分布律为:X 0 1P 1/2 1/2则随机变量Z=max{X,Y}的分布律为:______________________________.
随机变量X密度函数为f(x)=试求:(1)A值 (2)X的分布函数F(x) (3) E=(1/X2 ) (4) D(X)
已知连续随机变量X的概率密度函数为f(x)=,则X的数学期望为______;X的方差为______.
设随机变量X服从均值为10,均方差为0.02的正态分布,已知Φ(x)=du, Φ(2.5)=0.9938,则X落在区间(9.95,10.05)内的概率为______.
已知离散型随机变量X服从参数为2的泊松分布,即P{X=k}=2ke-2/k!,k=0,1,2,…,则随机变量Z=3X-2的期望E(Z)=________.
设随机变量X服从参数为1的指数分布,则数学期望E(X+e-2X )=__________.
随机变量z ~ N(2,32),则y=3z-2的数学期望为【 】
(X,Y)的联合概率分布为试求:(1)DX (2)DY (3)cov(X,Y)
设两个相互独立的随机变量X和Y分别服从正态分布N(0,1)和N(1,1),则【 】

