函数u=ln(x+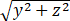
)在A(1,0,1)处沿A点指向B(3,-2,2)点方向的方向导数为________.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
微分方程y''-2y'+2y=ex的通解为____________.
设一平面经过原点及点P(6,-3,2)，且与平面4x-y+2z=8垂直，则此平面方程为______________.
设[(x+2a)/(x-a)]x=8，则a=________.
设随机变量X的概率密度为fX=，求随机变量Y=eX的概率密度fY (y).
设A是n阶矩阵，满足AAT=E(E是n阶单位矩阵，AT是A的转置矩阵)，|A|<0，求|A+E|.
设3阶实对称矩阵A的特征值为λ1=-1,λ2=λ3=1，对应于λ1的特征向量为ξ1=(0,1,1)T，求A.
设函数Q(x,y)在xOy平面上具有一阶连续偏导数，曲线积分∫L2xydx+Q(x,y)dy与路径无关，并且对任意t恒有2xydx+Q(x,y)dy=2xydx+Q(x,y)dy，求Q(x,y).
设曲线l位于xOy平面的第一象限内，l上任一点M处的切线与y轴总相交，交点记为A.已知||=||，且l过点(3/2,3/2)，求l的方程.
设参数方程x=f'(t),y=tf'(t)-f(t)，其中函数f(t)可以求导足够次数，求一阶导数dy/dx和二阶导数d2y/dx2.
设f,g为连续可微函数，u=f(x,xy),v=g(x+xy)，求∂u/∂x∙∂v/∂x
设u=yf(x/y)+xg(y/x)，其中函数f,g具有二阶连续导数，求x ∂2u/∂x2+y ∂2u/∂x∂y .
已知曲面z=4-x2-y2上点P处的切平面平行于平面2x+2y+z-1=0，则点P的坐标是【 】
设z=f(2x-y)+g(x,xy)，其中函数f(t)二阶可导，g(u,v)具有连续的二阶偏导数，求∂2z/∂x∂y.
设z=f(2x-y,ysinx)，其中f(u,v)具有连续的二阶偏导数，求∂2z/∂x∂y.
设n是曲面2x2+3y2+z2=6在点P(1,1,1)处的指向外侧的法向量，求函数u=/z在点P处沿方向n的方向导数.
函数u=ln(x2+y2+z2)在点M(1,2,-2)处的梯度 gradu|M=__________.
设f(x,y)=，问：f(x,y)在(0,0)处连续吗？方向可导吗？可微吗？
函数f(x,y)=x2+2y2在(0,1)的最大方向导数为______.
要使ξ1=,ξ2=都是方程组Ax=0的解，只要系数矩阵A为【 】
求微分方程x2y'+xy=y2满足初始条件y|x=1=1的特解.
设物体A从点(0,1)出发，以速度大小为常数v沿y轴正向运动，物体B从点(-1,0)与A同时出发，其速度大小为2v，方向始终指向A，试建立物体B的运动轨迹所满足的微分方程，并写出初始条件.
已知α=[1,2,3],β=[1,1/2,1/3]，设A=αTβ，其中αT是α的转置，则An=________________.