大学数学-竞赛试题(阿里巴巴 2020年3月向量空间)

证明题（2020年3月阿里巴巴）

设A=(a_ij)_n×n是一个由±1组成的n×n方阵(n>1).将A的n个行向量记为v₁,…,v_n.对于两个行行向量v=(a_i)_1≤i≤n与v'=(b_i)_1≤i≤n，定义

v*v'=(a_ib_i)_1≤i≤n

以及

v∙v'=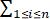a_ib_i

假设：

(1)对任意的i,j(1≤i,j≤n)，存在k(1≤k≤n)使得v_i*v_j=v_k；

(2)对任意的i,j(1≤i,j≤n,i≠j)， v_i∙v_j=0.

证明：

(i) A有一个行向量；对于A的另外任意一个行向量v_i，它有n/2个分量为1，n/2个分量为-1.

(ii)n是2的幂.

(ii)设n=2^m，则可以通过重新排列A的行与列，将A变为方阵

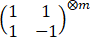
这里，X^⨂m==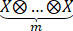

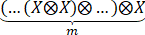
是方阵X的m次张量积：两个方阵X=(x_ij)_1≤i,j≤p与Y=(y_i'j')_{1≤i',j'≤q}的张量积被定义为一个pq×pq方阵

X⨂Y=(z_kl)_1≤kl≤pq

其中z_kl=x_ijy_i'j'，整数i,j,i',j'满足1≤i,j≤p,1≤i',j'<q，且由等式k=p(i'-1)+i与l=p(j'-1)+j唯一确定.

答案解析

(i)取一个行向量vi.由假设，存在k使得vk=vi*vi=.对于另外的任何一个向量vl=(a1,…,an)(l≠k)，由0=vk∙vl=ai 得vl，它有n/2个分量为1，n/2个分量为-1.(ii)&(iii)令G=(v1,…,vn).由假设，以运算*为乘法G是一个交换群，单位元是行vk=，由于v...

查看完整答案

讨论

向量空间

设B是秩为2的5×4矩阵，α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量，求Bx=0的解空间的一个标准正交基.

设R^3上的线性变换A(x)=x，则α=生成的A-循环不变空间的维数为________.

设A是n阶复方阵，V1是A的行向量生成的Cn的子空间，V2是A的列向量生成的Cn的子空间，则V1=V2.

设A是n维线性空间V的线性变换，则V=ImA⊕KerA.

已知A ̅和B ̅分别是三维空间中的矢量矩阵和单位方向矢量;A ̅=Ax+Ay+Az;( Ax=,Ay=,Az=B ̅=cosα+cosβ+cosγ;( cos2 α+cos2 β+cos2 γ=1)计算矩阵求和c=k(A ̅∙B ̅)k +2k (A ̅∙B ̅)2k.提示：首先考察(A ̅∙B ̅)2=?

在P[x]4定义内积：(f(x),g(x))=f(x)g(x) dx,f(x),g(x)∈P[x]4，并定义线性变换A:Aεi=ηi,i=1,2,3,4.ε1=1/2 (1+x+x2+x3 ),η1=2x+x2-x3 ε2=1/2 (-1-x+x2+x3 ),η2=-1-x2-2x3 ε3=1/2 (-1+x-x2+x3 ),η3=-2x-x2+x3 ε4=1/2 (-1+x+x2-x3 ),η4=1-4x-x2 求A的核空间的一个标准正交基.

已知全体实的2维向量关于下列运算构成R上的线性空间V：(a1,b1 )+(a2,b2 )=(a1+a2,b1+b2+a1 a2),k∙(a,b)=(ka,kb+(k(k-1))/2 a2).(1)求V的一组基;(2)定义变换A(a,b)=(a,a+b)，证明：A是一个线性变换；并求A在V的一组基下的矩阵表示.

设α1=(1,0,0,3),α2=(1,1,-1,2),α3=(1,2,a-3,1),α4=(1,2,-2,a),β=(0,1,b,-1)，问a,b为何值时(1) β能由α1,α2,α3,α4线性表示且表示唯一；(2) β不能由α1,α2,α3,α4线性表示；(3) β能由α1,α2,α3,α4线性表示但表示不唯一，并求一般表达式。

已知三维向量空间的基底为α1=(1,1,0)T,α2=(1,0,1)T,α3=(0,1,1)T，则向量β=(2,0,0)T在此基底下的坐标是____________.

设对角矩阵A的特征多项式为 φ(λ)=(λ-λi)ni （诸λi两两互异），求所有和A可交换的矩阵全体所组成的线性空间的维数.

向量组的线性相关性

设α1=,α2=,α3=，则三条直线a1 x+b1 y+c1=0,a2 x+b2 y+c2=0,a3 x+b3 y+c3=0,(其中ai2+bi2≠0,i=1,2,3)相交于一点的充要条件是【】

设A是n×m矩阵，B是m×n矩阵，其中n<m，E是n阶单位矩阵，若AB=E，证明B的列向量组线性无关.

设A是n阶矩阵，若存在正整数k，使线性方程组Akx=0有解向量α，且Ak-1α≠0，证明向量组α,Aα,…,Ak-1α是线性无关的.

已知向量α1=,α2=,β1=,β2=，若γ既可由α1,α2线性表示，也可由β1,β2线性表示，则γ=【】

已知向量α1=,α2=,α3=,β=,γ=k1 α1+k2 α2+k3 α3，若γTαi=βTαi (i=1,2,3)，则k12+k22+k32=______.

已知同维数的两个向量组有相同的秩，且其中之一可用另外一个线性表示，证明：这两个向量组等价。

四维矢量X采用列矩阵表示为：X=,其中，矢量X的四个分量x1,x2,x3,x4满足如下条件：，试证明：这样的四维矢量X存在“无穷多个”，并可一般表示为：X=ax1+bx2+1/2 x3;其中x1=,x2=,x3=;而a,b为“任意实数”.

设向量组A:α1,α2,… ,αs可以由向量组B:β1,β2,… ,βt线性表示且R(A)=R(B).证明向量组A与向量组B等价.

设xoy在平面上n个结点Mi(xi,yi ),i=1,2,…,n(n≥3).证明：M1,M2,…,Mn在同一条直线上⟺R=2.

已知向量组α1,α2,α3,α4线性无关，则向量组【】

分块矩阵

设A,B为n阶可逆矩阵，E为n阶单位矩阵，M*为M的伴随矩阵，则=【】

设A,B为n阶实矩阵，下列结论不成立的是【】

已知矩阵A=，若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵，则P,Q可以分别取【】

设A,B,C,D都是n×n矩阵，且|A|≠0,AC=CA，证明=|AD-CB|.

蚂蚁森林是全球最大的个人碳账户平台，该平台以量化方式记录每个人的低碳行为。当支付宝用户收集到足够的“能量”时，他/她可以向蚂蚁森林申请种植一棵真正的树。截至2019年4月22日(世界地球曰)，支付宝蚂蚁森林的5亿用户已经在中国西北地区种植了1亿棵真树，总面积为11.2万公顷，保护着总面积为1.2万公顷的保护地。1.本题两小问中考虑在一个3×4的长方形区域的每个小方格的中心点种树，要求在横、竖、斜3个方向上都不能存在连续的3颗(及以上)树。令1表示可以种树，0表示不可以种树。满足种树条件的示意图为不满足种树条件的示意图为(a)请问在一个3×4的区域里，最多能种多少颗树，并给出一种种植的方式。(b) 在满足上一问最多能种多少颗树答案的前提下，请问一共有多少种种法，给出思路和答案。2. 考虑一个由从左到右的n个小方格组成的1×n的区域，从左向右依次在每个小方格种一棵树，一共种n棵。树的种类只有两种：胡杨和樟子松。假设在第一个小方格种植的树是胡杨的概率是r。后续种树的规则为：如果前一个小方格种的是胡杨，则本格种胡杨的概率为s；如果前一个小方格种的是樟子松，则本格种樟子松的概率为t,0<r,s,t<1。(a)假设r=1/3,s+t≠1。是否存在s和t，使得对任意的i,2≤i≤n，在第i个小方格种植的树是胡杨的概率都等于一个跟i无关的常数？如果存在，请给出s和t的关系；如果不存在，请说明理由。(b) 假设r=1/3,s=3/4,t=4/5。假设我们观察到第2019个小方格里种植的树是胡杨，但我们观察不到在其它小方格里种植的是哪种树。请问在第一个小方格里种植的树是胡杨的概率是多少？3.为了种树的可持续发展控制成本，蚂蚁森林希望在知道用户申请数量之前从公益机构获得种植配额。令随机变量D1和D2分别表示支付宝用户对胡杨和樟子松的申请数量。将Di的分布函数记为Fi，其均值和方差分别表示为μi和σi2(i=1,2)。假设蚂蚁森林只知道μi和σi2 (i=1,2)但并不知道F的其它信息。蚂蚁森林需要确定两种树的配额，分别记为Qi (i=1,2)。由于环境的承受能力，种植的树木总数不能超过给定的常数M，即Q1+Q2≤M并且假设M≥μ1+μ2。已知两种树的订购成本分别为cQi (i=1,2)。如果预留配额Qi小于种树申请数量Di，即Qi≤Di，则增加额外成本m[Di-Qi ]+ (i=1,2)。这里[x]+≜max⁡{x,0}.m,c,μi,σi为已知常数且满足关系(m-c)/c>(σ1/μ1 )2>(σ2/μ2 )2.蚂蚁森林希望选择种树配额Qi≥0(i=1,2)使得在最坏情况下总成本的期望极小，其中最坏情况是针对所有可能的均值为μi、方差为σi2的分布函数Fi。从数学上讲，目标是求解以下优化问题：,(1)subject to Q1+Q2≤M,Q1,Q2≥0其中Fi是所有均值为μi、方差为σi2 (i=1,2)的累积分布函数的集合，其支撑集为非负数。问题：请求解问题(1)，推导最优种树配额Qi,i=1,2的显式表达式。

2019年第一届阿里巴巴数学竞赛的优胜者们在参加集训营的时候，集体送给主办方负责人的礼物，是一个有60个全等的三角形面的多面体。从图中我们可以看到，这个多面体的表面是60个全等的空间四边形拼接而成的。一个空间n边形是指由一个平面n边形沿若干条对角线做适当翻折（即在选定的对角线处形成适当的二面角)后得到的空间图形。两个空间图形全等指的是它们可以通过R3中的一个等距变换完全重合。一个多面体指的是一个空间有界区域，其边界可以由有限多个平面多边形沿公共边拼接而成。1. 判断题(4分) 我们知道2021=43×47.那么是否存在一个多面体，它的表面可以由43个全等的空间47边形拼接而成?2. 问答题(6分) 请对你的判断给出逻辑的解释。

面条是中华传统美食，花样不断翻新。清晨，擀宽面的张师傅别出心裁，把他的宽面条两头粘上，变成了宽面圈儿，如图：他平时切面条一样，把宽面圈儿沿着中心线切开，就得到两个完全同样的宽面圈儿，如图：张师傅灵机一动，重新将面条拧了一下，再两头粘上。这样竟然成了数学中常常讲到的莫比乌斯带（以德国数学家奥古斯特●莫比乌斯命名），如图：接着，他灵机两动，三动，直至n动。将宽面拧了两个，三下，直至n下，总以如图的右手内旋的方式来拧，然后照样地两头粘上。这些宽面圈儿在数学上还没有固定的名称。张师傅把莫比乌斯带称作1旋圈面，拧两下、三下的称作2旋、3旋圈面，总之，拧n下就是旋圈面；n为2、3、7的情形如图：起先没有拧就粘上的，普普通通，只称作平凡圈面，或者0旋圈面。在线师傅看来，不同旋数的圈面是彼此不同的（因为只在厨房里摆放来，摆放去，总不能把一种变成另一种）。张师傅把他的多旋圈面开店上架，一时网红。有人为百岁老人订制100旋圈面，有人为公司年会订制2019旋圈面，（张师傅拧得手都酸了）。试问：张师傅要是依旧沿中心线切开这两种圈面，分别会得到什么？【】

在一个虚拟的世界中，每个居民（设想为没有大小的几何点）依次编号为1,2,⋯.为了抗击某种疫情，这些居民要接种某疫苗，并在注射后在现场留观一段时间。现在假设留观的场所是平面上的一个半径为1/4的圆周。为了安全,要求第m号居民和第n居民之间的距离dm,n满足(m+n)dm,n≥1这里我们考虑的是圆周上的距离，也就是两点间劣弧的弧长。那么1.选择题(4分)下列选项（）符合实际情况。A 这个留观室最多能容纳8个居民B 这个留观室能容纳的居民个数有大于8的上限:C 这个留观室可以容纳任意多个居民。2.证明题(6分)证明你的论断。

去年，张师傅因为多旋圈面爆红，今年他来到了达摩院给扫地僧做面。某天，软件工程师小李跟张师傅吐槽工作。小李主要硏究和设计算法用于调节各种产品的参数。这样的参数一般可以通过极小化Rn上的某个损失函数f求得。在小李最近的一个项目中，这个损失函数是另外一个课题组提供的；出于安全考虑和技术原因，该课题组难以向小李给出此函数的内部细节，而只能提供一个接口用于计算任意x∈Rn处的函数值f(x)。所以，小李必须仅基于函数值来极小化f。而且，每次计算f的值都消耗不小的计算资源。好在该问题的维度n不是很高(10左右)。另外，提供函数的同事还告知小李不妨先假设f是光滑的。这个问题让张师傅想起了自己收藏的一台古董收音机。要在这台收音机上收听一个节目，你需要小心地来回拧一个调频旋钮，同时注意收音效果，直到达到最佳。在这过程中，没有人确切地知道旋钮的角度和收音效果之间的定量关系是什么。张师傅和小李意识到，极小化f不过就是调节一台有多个旋钮的机器：想象x的每一个分量由一个旋钮控制，而f(x)表示这台机器的某种性能，只要我们来回调整每个旋钮，同时监视f的值，应该就有希望找到最佳的x。受此启发，两人一起提出了极小化f的一个迭代算法，并命名为“自动前后调整算法”( Automated Forward/Backward Tuning，AFBT，算法1)。在第k次迭代中，AFBT通过前后调整xk的单个分量得2n个点{xk±tk ei:i=1,…,n}，其中tk为步长；然后，令yk为这些点中函数值最小的一个，并检査yk是否使f充分减小；若是，取xk+1=yk，并将步长增倍；否则，令xk+1=xk并将步长减半。在算法1中，ei表示Rn中的第i个坐标向量，它的第i个分量为1，其余皆为0； I(∙) 为指示函数——若f(xk )-f(yk)至少为tk之平方，则I[f(xk )-f(yk )≥tk2]取值为1，否则为0。1自动前后调整算法(AFBT)输入x0∈Rn,t0>0。对k=0,1,2,…，执行以下循环。1：yk≔argmin{f(y):y=xk±tk ei,i=1,…,n} #计算损失函数。2：sk≔I[f(xk )-f(yk )≥tk2] #是否充分下降？是：sk=1；否：sk=0。3：xk+1≔(1-sk ) xk+sk yk #更新迭代点。4：tk+1≔2(2sk-1 ) tk #更新步长。sk=1：步长增倍；sk=0：步长减半。现在，我们对损失函数f:Rn→R作出如下假设。假设1. f为凸函数，即对任何x,y∈Rn与α∈[0,1]都有f((1-α)x+αy)≤(1-α)f(x)+αf(y).假设2. f在Rn上可微且∇f在Rn上 L-Lipschitz连续。假设3. f的水平集有界，即对任意λ∈R，集合{x∈Rn:f(x)≤λ}皆有界。基于假设1与假设2，可以证明〈∇f(x),y-x〉≤f(y)-f(x)≤〈∇f(x),y-x〉+L/2 ‖x-y‖2对任何x,y∈Rn成立；假设1与假设3则保证f在Rn上取到有限的最小值f*。凸函数的更多性质可参考任何一本凸分析教科书。证明题(20分) 在假设1-3下，对于AFBT，证明f(xk)=f*.

令n为正整数。对任一正整数k，记0k=为k×k的零矩阵。令Y=为一个(2n+1)×(2n+1)矩阵，其中A=(xi,j)1≤i≤n,1≤j≤n+1是一个n×(n+1)实矩阵且At记A的转置矩阵，即(n+1)×n的矩阵，(j,i)处元素为xi,j.(i)证明题（10分）称复数λ为k×k矩阵X的一个特征值，如果存在非零列向量v=(x1,…,xk)t使得Xv=λv.证明：0是Y的特征值且Y的其他特征值形如±，其中非负实数λ是AAt的特征值。(ii)证明题（15分）令n=3且a1,a2,a3,a4是4个互不相等的正实数。记a=以及xi,j=ai δi,j+aj δ4,j-1/a2 (ai2+a42)aj(1≤i≤3,1≤j≤4)，其中δi,j= .证明：Y有7个互不相等的特征值。