已知矩阵:
A=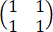 ,B=
,B=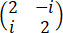 ,C=
,C=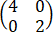
计算:(cosα∙A+cosβ∙B+cosγ∙C)3=?其中,cos2 α+cos2 β+cos2 γ=1,cosα+2cosβ+3cosγ=√3/3.
提示:设E= ,并引入三个矩阵:A'=A-E,B'=B-2E,C'=C-3E [注意:(cosα∙A'+cosβ∙B'+cosγ∙C')2=?]后,再作计算.
,并引入三个矩阵:A'=A-E,B'=B-2E,C'=C-3E [注意:(cosα∙A'+cosβ∙B'+cosγ∙C')2=?]后,再作计算.
已知矩阵:
A=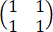 ,B=
,B=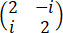 ,C=
,C=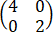
计算:(cosα∙A+cosβ∙B+cosγ∙C)3=?其中,cos2 α+cos2 β+cos2 γ=1,cosα+2cosβ+3cosγ=√3/3.
提示:设E= ,并引入三个矩阵:A'=A-E,B'=B-2E,C'=C-3E [注意:(cosα∙A'+cosβ∙B'+cosγ∙C')2=?]后,再作计算.
,并引入三个矩阵:A'=A-E,B'=B-2E,C'=C-3E [注意:(cosα∙A'+cosβ∙B'+cosγ∙C')2=?]后,再作计算.
暂无答案
证明:任一可逆的实矩阵A可以表示成A=QB,其中Q为正交矩阵,B是主对角线上元素均为正的三角形矩阵:B=,bii>0,且此表示式是惟一的。
设A∈Rm×n,rankA=r,证明存在可逆矩阵M∈Rm×m及正交矩阵P∈Rn×n,使得MAP= 其中Rm×n表示 m×n实数矩阵空间,Ir表示r×r单位矩阵,C∈Rr×(n-r)。
设A为3阶矩阵,交换A的第2行和第3行,再将第2列的-1倍加第1列,得到矩阵,则A-1的迹tr(A-1)=__________.
方阵A=,而n≥2为整数,则A2-2An-1=__________。
已知A=,B=满足(E-A-1B) XT=A-1(其中E为单位阵),试求X。
设A为m×n且秩为s的矩阵,X为p×m的列满秩矩阵,即r(X)=m,而Y为n×q的行满秩矩阵,即r(Y)=n。证明:r(A)=r(XA)=r(AY)=r(XAY)其中符号r(T)表示矩阵T的秩。
考虑循环矩阵A=证明:(1) A=a0 In+a1 T+a2 T2+⋯+an-1 Tn-1,其中T=In表示n×n单位矩阵。(2) T相似于对角矩阵。(3) A相似于对角矩阵。
设A,B,C,D都是n×n矩阵,且|A|≠0,AC=CA,证明=|AD-CB|.
设矩阵T=,T以及D可逆,证明(A-BD-1 C)-1存在,并求T-1,其中A,B,C,D为适当维度的矩阵。
设A是n级实对称矩阵,证明rank(A)=n的充要条件是:存在实对称矩阵B使AB+B'A是正定矩阵。
设S1,S3为实对称矩阵,S2为实矩阵,则矩阵S=为正定矩阵的充要条件为矩阵S3与矩阵S1-S2 S3-1 S2'皆为正定矩阵。
设A为实对称矩阵。证明当实数t充分大之后,tI+A是正定矩阵,其中I表示单位矩阵。
设B为一r×r矩阵,C为一r×n矩阵.如果BC=C,问B=E是否成立?若成立,证明之;若不成立,举出反例,并给出使B=E的充要条件。其中E为单位矩阵.