在直角坐标系下，已知一点M0 (1,2,0)和一条直线L: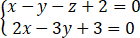
，求M0到L的距离，并写出过M0且与L垂直相交的直线方程.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设V是欧氏空间，W是V的子空间，V中的向量α不在W中，问是否存在α0∈W，使得α-α0与W的任意向量都正交？如果不存在，举出例子；如果存在，说明理由并讨论其唯一性.
设A是n阶初满秩矩阵，证明：存在正交矩阵P1,P2使得P1-1AP2=其中λi>0(i=1,2,⋯,n).
证明：秩等于r的矩阵可以表示为r个秩等于1的矩阵之和，但不能表示为少于r个秩等于1的矩阵之和.
设f(x)是有理数域Q上的一个m次多项式，n是大于m的正整数，证明不是f(x)的实根.
设矩阵A=,β=，已知线性方程组AX=β有解但不唯一.(1)求a的值；(2)求一个正交矩阵Q，使得QTAQ为对角矩阵.
设函数f:[0,1]→R是连续的且在(0,1)上可微，若f满足：(1) f(0)=0；(2)存在常数M>0使得|f'(x)|≤M|f(x)|对任意x∈(0,1)成立.证明：在[0,1]上f(x)=0.
设f(x),g(x)在(-∞,+∞)上连续，且[f(x)-g(x)]=0.证明：f(x)在(-∞,+∞)上一致连续当且仅当g(x)在(-∞,+∞)上一致连续.
证明：当x>0时，ln√x=1/(2n-1) ((x-1)/(1+x))2n-1 ，并讨论1/(2n-1) ((x-1)/(1+x))2n-1关于x∈(0,+∞)是否一致收敛.
证明双曲抛物面同族的任意两条直母线必是异面直线，且同族的全体直母线平行于同一个平面.
计算R3中曲面(x12)/(a12 )+(x22)/(a22 )=(x32)/(a32 )与超平面x3=a3所围锥体的体积，a1,a2,a3>0.
设空间直角坐标系中的四点A(1,1,1),B(1,2,3),C(1,2,4),D(2,3,4),则点A到平面BCD的距离d=__________.
设一平面经过原点及点P(6,-3,2)，且与平面4x-y+2z=8垂直，则此平面方程为______________.
过点M(1,2,-1)且与直线垂直的平面方程是__________.
已知两条直线的方程是 l1:(x-1)/1=(y-2)/0=(z-3)/(-1);l2:(x+2)/2=(y-1)/1=z/1.则过l1且平行于l2的平面方程是____________.
在上半平面求一条向上凹的曲线，其上任一点P(x,y)处的曲率等于此曲线在该点的法线段PQ长度的倒数(Q是法线与x轴的交点)，且曲线在点(1,1)处的切线与x轴平行.
设直线l1:(x-1)/1=(y-5)/(-2)=(z+8)/1与l2:则l1与l2的夹角为【 】
设有直线l:及平面π:4x-2y+z-2=0，则直线l【 】
计算∫L(x²+y²+z²)ds，其中L:x=acost,y=asint,z=bt,t∈[0,2π].
设u=u(x,y,z),v=v(x,y,z),w=w(x,y,z)由x=u+v+w,y=uv+uw+vw,z=uvw确定，求∂u/∂x,∂u/∂y,∂u/∂z.
计算∫Γex(1-cosy)dx-ex(y-siny)dy，其中Γ:y=sinx,x∈[0,π]，方向从(π,0)到(0,0).
设y=y(x)由方程y²-x+siny=0(x≥1)确定，且y=y(x)经过(π²,π).试讨论y(x)在(1,+∞)上零点的个数，并求y(x).