大学数学-考研试题(东北师范大学 2023年数列极限)

计算题（2023年东北师范大学）

求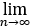(1²+3²+⋯+(2n-1)²)/n³

答案解析

暂无答案

讨论

大学数学

设某种元器件的使用寿命T的分布函数为F(t)=其中θ,m为参数且均大于零.(1)求概率P{T>t}与P{T>s+t|T>s}，其中s>0,t>0.(2)任取n个这种元件做寿命实验，测得它们的寿命分别为t1,⋯,tn，若m已知，求θ的最大似然估计值.

设随机变量X1,X2,X3相互独立，其中X1,X2均服从标准正态分布，X3的概率分布为P{X3=0}=P{X3=1}=1/2,Y=X3 X1+(1-X3 ) X2(1)求二维随机变量(X1,Y)的分布函数，结果用标准正态分布函数Φ(x)表示；(2)证明随机变量Y服从标准正态分布.

设A为2阶矩阵，P(α,Aα)，其中α是非零向量且不是A的特征向量(1)证明P为可逆矩阵；(2)若A²α+Aα-6α=0，求P-1AP，并判断A是否相似于对角矩阵.

设二次型f(x1,x2 )=x1²-4x1 x2+4x2²经正交变换=Q化为二次型g(y1,y2 )=ay1²+4y1 y2+by2²，其中a≥b.(1)求a,b的值；(2)求正交矩阵Q.

设f(x)在[0,2]上具有连续导数，f(0)=f(2)=0,M=max⁡|f(x)|,x∈[0,2]，证明：(1)∃ξ∈[0,2]，使得|f'(ξ)|≥M；(2)若∀x∈[0,2],|f'(x)|≤M，则M=0.

设Σ为曲面z=(1≤x²+y²≤4)的下侧，f(x)是连续函数，计算I=∬Σ(xf(xy)+2x-y)dydz+(yf(xy)+2y+x)dzdx+(zf(xy)+z)dxdy.

设数列{an}满足a1=1,(n+1) an+1=(n+1/2) an，证明：当|x|<1时，幂级数an xn 收敛，并求其和函数.

计算曲线积分I=∫(4x-y)/(4x²+y² ) dx+(x+y)/(4x²+y² ) dy，其中I是曲线L:x²+y²=2，方向为逆时针方向.

求f(x,y)=x³+8y³-xy的极值.

设X服从区间(-π/2,π/2)的均匀分布，Y=sinX，则Cov(X,Y)=________.

数列极限

已知正项级数an 收敛，数列{xn}满足|xn+1-xn |≤a_n,∀n≥1.证明：{xn}收敛.

设x1=10,xn+1=(n=1,2,⋯)，试证数列{xn}的极限存在，并求此极限.

求⁡[sin⁡(π/n)/(n+1)+sin(2π/n)/(n+1/2)+⋯+sinπ/(n+1/n)]

已知an=a≠0，试用ε-N语言证明：1/an =1/a.

证明数列{sinn}发散.

设数列{xn}满足1/xn+1 +lnxn<1，证明：xn存在，并求之.(已知：1/x+lnx≥1)

求极限(1+++⋯+)/n.

求极限nxnexdx.

求证：((cosx)ndx)1/n =1

求证：(n/3-k2/n2 )=-1/2.

函数与极限

当x→0+时，下列无穷小阶数最高的是【】

(1/(ex-1)-1/ln⁡(1+x) )=______.

东北师范大学两个重要极限

设y=y(x)由方程y²-x+siny=0(x≥1)确定，且y=y(x)经过(π²,π).试讨论y(x)在(1,+∞)上零点的个数，并求y(x).

设f(x)在[a,b)上严格单调，xn∈(a,b)，证明：如果f(xn)=f(a)，则xn=a.

设f(x),g(x)在(-∞,+∞)上连续，且[f(x)-g(x)]=0.证明：f(x)在(-∞,+∞)上一致连续当且仅当g(x)在(-∞,+∞)上一致连续.

f(x)=|xsinx| ecosx,-∞<x<+∞是【】

设函数f(x)=，则函数f[f(x)]=__________.

设 f(x) 是连续函数，F(x)是 f(x)的原函数，则【】

江苏省数列极限存在准则