求证：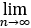
(n/3-
k2/n2 )=-1/2.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
证明题（2022年吉林大学）
答案解析
由于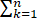
k2 =(n(n+1)(2n+1))/6
所以，原式=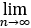(n/3-(n(n+1)(2n+1))/6)=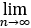(-3n2-n)/(6n2)=-1/2.
讨论
已知an=-(-1)n/n(n=1,2,…)，则{an}【 】
对有界数列{xn}，下面哪个说法可作为xn=L的定义【 】（此题不全，待更新）
设f(x)=sin(a1 x)+sin(a2 x)+sin(a3 x),a1,a2,a3>0.证明：存在数列{tn}使得tn=+∞且f(x+tn)=f(x)对∀x∈R一致成立.
已知an=+∞，证明(a1+a2+⋯+an)/n=+∞，并举例说明反过来不成立.
设数列{xn}满足1/xn+1 +lnxn<1，证明：xn存在，并求之.(已知：1/x+lnx≥1)
设函数f(x)在x=a可导，且f(a)≠0，则=__________。