设某种元器件的使用寿命T的分布函数为
F(t)=
其中θ,m为参数且均大于零.
(1)求概率P{T>t}与P{T>s+t|T>s},其中s>0,t>0.
(2)任取n个这种元件做寿命实验,测得它们的寿命分别为t1,⋯,tn,若m已知,求θ的最大似然估计值.
设某种元器件的使用寿命T的分布函数为
F(t)=
其中θ,m为参数且均大于零.
(1)求概率P{T>t}与P{T>s+t|T>s},其中s>0,t>0.
(2)任取n个这种元件做寿命实验,测得它们的寿命分别为t1,⋯,tn,若m已知,求θ的最大似然估计值.
(1) P{T>t}=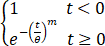
P{T>t+s│T>s}=
(2)θ的最大似然估计值为
(详细解答过程见word版)
设A为2阶矩阵,P(α,Aα),其中α是非零向量且不是A的特征向量(1)证明P为可逆矩阵;(2)若A²α+Aα-6α=0,求P-1AP,并判断A是否相似于对角矩阵.
设二次型f(x1,x2 )=x1²-4x1 x2+4x2²经正交变换=Q化为二次型g(y1,y2 )=ay1²+4y1 y2+by2²,其中a≥b.(1)求a,b的值;(2)求正交矩阵Q.
设Σ为曲面z=(1≤x²+y²≤4)的下侧,f(x)是连续函数,计算I=∬Σ(xf(xy)+2x-y)dydz+(yf(xy)+2y+x)dzdx+(zf(xy)+z)dxdy.
设数列{an}满足a1=1,(n+1) an+1=(n+1/2) an,证明:当|x|<1时,幂级数an xn 收敛,并求其和函数.
计算曲线积分I=∫(4x-y)/(4x²+y² ) dx+(x+y)/(4x²+y² ) dy,其中I是曲线L:x²+y²=2,方向为逆时针方向.
总体X的概率分布为P{X=1}=(1-θ)/2,P{X=1}=P{X=3}=(1+θ)/4,利用来自总体X的样本观察值1,3,2,2,1,3,1,2可得θ的最大似然估计值为【 】
设总体X的概率密度为f(x)=,其中θ>-1是未知参数.X1,X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.
设X1,X2为来自总体N(μ,σ2)的简单随机样本,其中σ(σ>0)是未知参数.若σ ̂=a|X1-X2 |为σ的无偏估计,则a=【 】
设函数f(x)在区间(-1,1)内有定义,且f(x)=0,则【 】
设函数f(x,y)在点(0,0)处可微,f(0,0)=0,n= (∂f/∂x,∂f/∂y,-1)|(0,0),非零向量r与n垂直,则【 】
设A,B,C为三个随机事件,且P(A)=P(B)=P(C)=1/4,P(AB)=0,P(AC)=P(BC)=1/12,则A,B,C中恰有一个事件发生的概率为【 】
设X1,X2,⋯,X100为来自总体X的简单随机样本,其中P{X=0}=P{X=1}=1/2,Φ(x)表示标准正态分布函数,则利用中心极限定理可得P{Xi≤55}的近似值为【 】
(1/(ex-1)-1/ln(1+x) )=______.
若函数f(x)满足f'' (x)+af' (x)+f(x)=0(a>0),且f(0)=m,f' (0)=n,则f(x)dx=________.
设函数f(x,y)=ext²dt,则∂²f/∂x∂y|(1,1)=______
设有直线l:及平面π:4x-2y+z-2=0,则直线l【 】
设函数f(x)在[0,1]上f'' (x)>0,则f' (0),f' (1),f(1)-f(0)或f(0)-f(1)的大小顺序是【 】