设总体X的概率密度为
f(x)=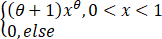 ,其中θ>-1是未知参数.
,其中θ>-1是未知参数.
X1,X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.
设总体X的概率密度为
f(x)=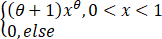 ,其中θ>-1是未知参数.
,其中θ>-1是未知参数.
X1,X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.
总体X的数学期望为E(X)=xf(x) dx=(θ+1) xθ+1 dx=(θ+1)/(θ+2)∙ xθ+2 =(θ+1)/(θ+2).令E(X)=X ̅=(θ+1)/(θ+2),解得θ=(2X ̅-1)/(1-X ̅ ),因此θ的矩法估计量为 θ ̂=(2 1/nXi-1)/(1-1/n Xi ).设x1,x2,…,xn是相应于样本X1,X2,...
查看完整答案从学校乘汽车到火车站的途中有3个交通岗,假设在各交通岗遇到红灯的事件是相互独立的,并且概率都是2/5.设X为途中遇到红灯的次数,求随机变量X的分布律、分布函数和数学期望.
设A是n阶可逆方阵,将A的第i行和第j行对换后得到的矩阵记为B.(1)证明B可逆;(2)求AB-1.
已知ξ=是矩阵A=的一个特征向量.(1)试确定参数a,b及特征向量ξ所对应的特征值;(2)问A能否相似于对角阵?说明理由.
设B是秩为2的5×4矩阵,α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量,求Bx=0的解空间的一个标准正交基.
设a1=2,an+1=1/2(an+1/an )(n=1,2,…),证明:(1) an 存在;(2)级数(an/an+1 -1)收敛.
设f(x)连续,φ(x)=f(xt)dt,且f(x)/x=A(A为常数),求φ'(x)并讨论φ'(x)在x=0处的连续性.
设函数f(u)具有二阶连续导数,而z=f(exsiny)满足方程∂2z/∂x2+∂2z/∂y2=e2x z,求f(u).
设直线l:在平面π上,且平面π与曲面z=x2+y2相切于点(1,-2,5),求a,b的值.
计算曲线积分∮C(z-y)dx+(x-z)dy+(x-y)dz,其中C是曲线从z轴正向往z轴负向看,C的方向是顺时针的.
总体X的概率分布为P{X=1}=(1-θ)/2,P{X=1}=P{X=3}=(1+θ)/4,利用来自总体X的样本观察值1,3,2,2,1,3,1,2可得θ的最大似然估计值为【 】
设X1,X2为来自总体N(μ,σ2)的简单随机样本,其中σ(σ>0)是未知参数.若σ ̂=a|X1-X2 |为σ的无偏估计,则a=【 】
设随机事件A,B及其和事件A∪B的概率分别是0.4,0.3,0.6,若B ̅表示B的对立事件,那么积事件AB ̅的概率P(AB ̅ )=________.
已知β1,β2是非齐次线性方程组Ax=b的两个不同的解,α1,α2是对应齐次线性方程组Ax=0的基础解系,k1,k2为任意常数,则方程组Ax=b的通解(一般解)必是【 】
设4阶矩阵B=,C=,且矩阵A满足关系式A(E-C-1 B)T CT=E,其中E为4阶单位矩阵,C-1表示 C的逆矩阵,CT表示 C的转置矩阵,将上述关系式化简并求矩阵A.
随机地向半圆0<y<(a为常数)内掷一点,点落在半圆内任何区域的概率与该区域的面积与正比,则原点和该点的连续与x轴的夹角小于π/4的概率为__________.
设n阶方阵A,B,C满足关系式ABC=E,其中E是n阶单位矩阵,则必有【 】
设A是n阶正定矩阵,E是n阶单位矩阵,证明A+E的行列式大于1.
设n阶矩阵A的各行元素之和均为零,且A的秩为n-1,则线性方程组Ax=0的通解为____________.
设物体A从点(0,1)出发,以速度大小为常数v沿y轴正向运动,物体B从点(-1,0)与A同时出发,其速度大小为2v,方向始终指向A,试建立物体B的运动轨迹所满足的微分方程,并写出初始条件.
已知α=[1,2,3],β=[1,1/2,1/3],设A=αTβ,其中αT是α的转置,则An=________________.