-
关注“优题吧”，分配平台账号.
考研2024年理工数学Ⅰ( )
设总体X服从[0,θ]上的均匀分布，其中θ∈(0,+∞)为未知参数，X1,X2,⋯,Xn是来自总体X的简单随机样本，记
X(n)=max{X1,X2,⋯,Xn },Tc=cX(n)
(1)求c，使得Tc是θ的无偏估计；
(2)记h(c)=E(Tc-θ)²，求c使得h(c)最小.
解答过程见word版
考研2020年理工数学Ⅰ( )
设某种元器件的使用寿命T的分布函数为
F(t)=
其中θ,m为参数且均大于零.
(1)求概率P{T>t}与P{T>s+t|T>s}，其中s>0,t>0.
(2)任取n个这种元件做寿命实验，测得它们的寿命分别为t1,⋯,tn，若m已知，求θ的最大似然估计值.
(1) P{T>t}=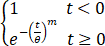
P{T>t+s│T>s}=
(2)θ的最大似然估计值为
(详细解答过程见word版)
考研2023年理工数学Ⅰ( )
设X1,X2为来自总体N(μ,σ2)的简单随机样本，其中σ(σ>0)是未知参数.若σ ̂=a|X1-X2 |为σ的无偏估计，则a=【 】
A、√π/2
B、√2π/2
C、√π
D、√2π
考研2022年理工数学Ⅰ( )
设X1,X2,…,Xn为来自均值为θ的指数分布总体的简单随机样本，Y1,Y2,…,Ym为来自均值为2θ的指数分布总体的简单随机样本，且两样本相互独立，其中θ(θ>0)是未知参数.利用样本X1,X2,…,Xn,Y1,Y2,…,Ym求θ的最大似然估计量θ ̂，并求D(θ ̂).
由题知，X的概率密度为fX (x,θ)=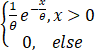
,
Y的概率密度为fY (y,θ)=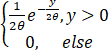
.
令L=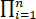
fX (xi,θ)
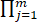fY (yj,θ) =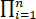1/θ e-xi/θ 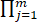1/2θ e-yj/2θ (xi>0,yj>0,i=1,2,…,n,j=1,2,…,m).
则lnL=
(-lnθ-xi/θ)+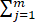
(ln 1/2-lnθ-yj/2θ).
∴dlnL/dθ=(-1/θ+xi/θ2 )+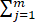(-1/θ+yj/(2θ2 ))=-(m+n)/θ+xi/θ2 +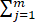yj/(2θ2 )=0
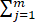⟹θ ̂=1/(m+n)(xi +1/2 yj ).
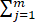∴θ的最大似然估计量为θ ̂=1/(m+n)(xi +1/2 yj ).
D(θ ̂ )=1/(m+n)2 (DXi+1/4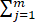DYj )=1/(m+n)2 (nDX+1/4 mDY)
=1/(m+n)2 (nθ2+1/4 m4θ2 )=θ2/(m+n).
考研1997年理工数学Ⅰ( )
设总体X的概率密度为
f(x)=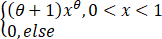
,其中θ>-1是未知参数.
X1,X2,…,Xn是来自总体X的一个容量为n的简单随机样本，分别用矩估计法和极大似然估计法求θ的估计量.
总体X的数学期望为
E(X)=
xf(x) dx=
(θ+1) xθ+1 dx=(θ+1)/(θ+2)∙ xθ+2 
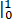=(θ+1)/(θ+2).
令E(X)=X ̅=(θ+1)/(θ+2)，解得θ=(2X ̅-1)/(1-X ̅ ),
因此θ的矩法估计量为 θ ̂=(2 1/n
Xi-1)/(1-1/n Xi ).
设x1,x2,…,xn是相应于样本X1,X2,…,Xn的一组观测值，侧似然函数为
L(θ)=L(x1,x2,…,xn;θ)=
f(xi )=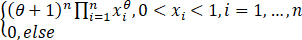
=
,
当0<xi<1(i=1,…,n)时，L(θ)>0，且lnL(θ)=nln(θ+1)+θlnxi .
令dlnL(θ)/dθ=n/(θ+1)+lnxi =0，解得θ=-1-n/(lnxi ).
故θ的最大似然估计为θ ̂=-1-n/(lnXi ).