若函数f(x)满足f'' (x)+af' (x)+f(x)=0(a>0)，且f(0)=m,f' (0)=n，则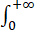
f(x)dx=________.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
填空题（2020年理工数学Ⅰ）
答案解析
n+am
【解析】
详细过程见word版
讨论
(1/(ex-1)-1/ln(1+x) )=______.
设X1,X2,⋯,X100为来自总体X的简单随机样本，其中P{X=0}=P{X=1}=1/2,Φ(x)表示标准正态分布函数，则利用中心极限定理可得P{Xi≤55}的近似值为【 】
设A,B,C为三个随机事件，且P(A)=P(B)=P(C)=1/4,P(AB)=0,P(AC)=P(BC)=1/12，则A,B,C中恰有一个事件发生的概率为【 】
设函数f(x,y)在点(0,0)处可微，f(0,0)=0,n= (∂f/∂x,∂f/∂y,-1)|(0,0)，非零向量r与n垂直，则【 】
微分方程y''-y=ex+1的一个特解应具有形式（式中a,b为常数）【 】
设对任意x>0，曲线y=f(x)在点(x,f(x))处的切线在y轴上的截距等于1/x f(t)dt，求f(x)的一般表达式.
求微分方程y''+4y'+4y=eax的通解，其中a为实数.
已知函数y=y(x)在任意点x处的增量Δy=yΔx/(1+x2)+α，且当Δx→0时，α是∆x(∆x→0)的高阶无穷小，y(0)=π，则y(1)等于【 】
设函数y=y(x)满足微分方程y''-3y'+2y=2ex，其图形在点(0,1)处的切线与曲线y=x2-x+1在该点处的切线重合，求函数y=y(x).
设线性无关的函数y1,y2,y3都是二阶非齐次线性方程y''+p(x) y'+q(x)y=f(x)的解，C1,C2是任意常数，则该非齐次方程的通解是【 】
设f(x)=sinx-(x-t)f(t)dt，其中f为连续函数，求f(x).
设函数f(x,y)=ext²dt，则∂²f/∂x∂y|(1,1)=______
设X服从区间(-π/2,π/2)的均匀分布，Y=sinX，则Cov(X,Y)=________.
计算曲线积分I=∫(4x-y)/(4x²+y² ) dx+(x+y)/(4x²+y² ) dy，其中I是曲线L:x²+y²=2，方向为逆时针方向.
设数列{an}满足a1=1,(n+1) an+1=(n+1/2) an，证明：当|x|<1时，幂级数an xn 收敛，并求其和函数.
设Σ为曲面z=(1≤x²+y²≤4)的下侧，f(x)是连续函数，计算I=∬Σ(xf(xy)+2x-y)dydz+(yf(xy)+2y+x)dzdx+(zf(xy)+z)dxdy.