设f(x)是有理数域Q上的一个m次多项式，n是大于m的正整数，证明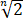
不是f(x)的实根.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设矩阵A=,β=，已知线性方程组AX=β有解但不唯一.(1)求a的值；(2)求一个正交矩阵Q，使得QTAQ为对角矩阵.
设函数f:[0,1]→R是连续的且在(0,1)上可微，若f满足：(1) f(0)=0；(2)存在常数M>0使得|f'(x)|≤M|f(x)|对任意x∈(0,1)成立.证明：在[0,1]上f(x)=0.
设f(x),g(x)在(-∞,+∞)上连续，且[f(x)-g(x)]=0.证明：f(x)在(-∞,+∞)上一致连续当且仅当g(x)在(-∞,+∞)上一致连续.
证明：当x>0时，ln√x=1/(2n-1) ((x-1)/(1+x))2n-1 ，并讨论1/(2n-1) ((x-1)/(1+x))2n-1关于x∈(0,+∞)是否一致收敛.
已知正项级数an 收敛，数列{xn}满足|xn+1-xn |≤a_n,∀n≥1.证明：{xn}收敛.
设f(x)在[a,b)上严格单调，xn∈(a,b)，证明：如果f(xn)=f(a)，则xn=a.
设y=y(x)由方程y²-x+siny=0(x≥1)确定，且y=y(x)经过(π²,π).试讨论y(x)在(1,+∞)上零点的个数，并求y(x).
计算∫Γex(1-cosy)dx-ex(y-siny)dy，其中Γ:y=sinx,x∈[0,π]，方向从(π,0)到(0,0).
设u=u(x,y,z),v=v(x,y,z),w=w(x,y,z)由x=u+v+w,y=uv+uw+vw,z=uvw确定，求∂u/∂x,∂u/∂y,∂u/∂z.
证明：如果d(x)|f(x),d(x)|g(x)，且d(x)是f(x)与g(x)的一个组合，那么d(x)是f(x)与g(x)的一个最大公因式.
设A∈Cn×n,W={f(A):f(x)∈P[x]},m(x)是A的最小多项式，证明：W的维数=∂(m(x))，其中∂(m(x))表示m(x)的最高次数.
若不可约多项式p(x)是f(k)(x)的s重因子，且p(x)|f(x)，那么p(x)________ f(x)的s+k重因子.
设f(x)=x3+6x2+3px+8，试确定p的值使f(x)有重根并求其根.
设复系数多项式f(x)在x=1处的导数f'(1)≠0.证明：存在n阶复方阵A使得f(A)=f(1)J，其中J=是n阶Jordan块.
设A=(aij)n×n，且行列式≠0,1≤k≤n.证明存在下三角形矩阵Bn×n，使BA为上三角形矩阵。
设f(x)是有理数域Q上的一个m次多项式，n是大于m的正整数，证明不是f(x)的实根.