设直线
l1:(x-1)/1=(y-5)/(-2)=(z+8)/1与l2: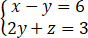
则l1与l2的夹角为【 】
A、π/6
B、π/4
C、π/3
D、π/2
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
双纽线(x2+y2)2=x2-y2所围成的区域面积可用定积分表示为【 】
设f(x)=sint2dt,g(x)=x3+x4，则当x→0时，f(x)是g(x)的【 】
设随机变量X服从(0,2)上的均匀分布，则随机变量Y=X2在(0,4)内的概率分布密度fY(y)=__________.
一批产品共有10个正品和2个次品，任意抽取两次，每次抽1个，抽出后不再放回，则第二次抽出的是次品的概率为__________.
设n阶矩阵A的各行元素之和均为零，且A的秩为n-1，则线性方程组Ax=0的通解为____________.
设数量场u=ln，则div(gradu)=________________.
设函数f(x)=πx+x2 (-π<x<π)的傅里叶级数展开式为a0/2+(ancosnx+bnsinnx)，其中系数b3的值为__________.
由曲线绕y轴旋转一周得到的旋转柱面在点(0,√3,√2)处的指向外侧的单位法向量为__________.
函数F(x)=(2-1/√t) dt(x>0)的单调减少区间为__________.
设随机变量X与Y独立，X服从正态分布N(μ,σ2)，Y服从[-π,π]上的均匀分布，试求Z=X+Y的概率分布密度（计算结果用标准正态分布函数Φ(x)表示，其中Φ(x)=dt）.
已知α=(1,2,3);β=(1,1/2,1/3)，设A=αTβ，则An=__________。
与两直线及(x+1)/1=(y+2)/2=(z-1)/1都平行且过原点的平面方程为______________.
过点M(1,2,-1)且与直线垂直的平面方程是__________.
已知两条直线的方程是 l1:(x-1)/1=(y-2)/0=(z-3)/(-1);l2:(x+2)/2=(y-1)/1=z/1.则过l1且平行于l2的平面方程是____________.
在上半平面求一条向上凹的曲线，其上任一点P(x,y)处的曲率等于此曲线在该点的法线段PQ长度的倒数(Q是法线与x轴的交点)，且曲线在点(1,1)处的切线与x轴平行.
设向量组α1,α2,α3线性相关，α2,α3,α4线性无关，问：(1) α1能否由α2,α3线性表出？证明你的结论.(2) α4能否由α1,α2,α3线性表出？证明你的结论.
求直线l:(x-1)/1=y/1=(z-1)/-1在平面π:x-y+2z-1=0上的投影直线l0的方程，并求l0绕y轴旋转一周所成曲面的方程.
设空间直角坐标系中的四点A(1,1,1),B(1,2,3),C(1,2,4),D(2,3,4),则点A到平面BCD的距离d=__________.
设有直线l:及平面π:4x-2y+z-2=0，则直线l【 】
设f(x)是周期为2的周期函数，它在区间(-1,1]上定义为f(x)=，则f(x)的傅里叶级数在x=1处收敛于______.
设4阶矩阵A=(α,γ2,γ3,γ4 ),B=(β,γ2,γ3,γ4)，其中α,β,γ2,γ3,γ4均为四维列向量，且已知行列式|A|=4,|B|=1，则行列式|A+B|=________.
若函数y=f(x)可导，且f'(x0)=1/2，则当∆x→0时，该函数在x=x0处的微分dy是【 】