大学数学-考研试题(理工数学Ⅱ 2024年 n维向量)

填空题（2024年理工数学Ⅱ）

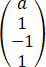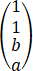设向量α₁=,α₂=,α₃=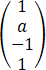，若α₁,α₂,α₃线性相关，且其中任意两个向量均线性无关，则ab=__________.

答案解析

-4

讨论

大学数学

某物体以速度v(t)=t+ksinπt做直线运动，若它从t=0到t=3的时间段内平均速度是5/2，则k=__________.

已知函数f(x)=x²(ex+1)，则f(5)(1)=___________.

微分方程y'=1/(x+y)² 满足 y(1)=0的解为___________.

函数f(x,y)=2x³-9x²-6y4+12x+24y的极值点是__________.

曲线y²=x在点(0,0)处的曲率圆方程为____________________.

设A，B为2阶矩阵，且AB = BA，则“A有两个不相等的特征值”是“B可对角化”的【】

设A为4阶矩阵，A*为A的伴随矩阵，若A(A-A*)=0，且A≠A*，则r(A)取值为【】

设A为3阶矩阵，P=，若PT AP²=，则A=【】

设非负函数f(x)在[0,+∞)上连续，给出以下三个命题：①若f² (x)收敛，则f(x)收敛.②若存在p>1，使得xp f(x)存在，则f(x)收敛.③若f(x)收敛，则存在p>1，使得xp f(x)存在.其中真命题个数为【】

设f(x,y)是连续函数，则dxf(x,y)dy=【】

n维向量

已知直线L1:(x-a2)/a1 =(y-b2)/b1 =(2-c2)/c1 与直线L2:(x-a3)/a2 =(y-b3)/b2 =(2-c3)/c2 相交与一点，法向量αi=,i=1,2,3，则【】

四维矢量X采用列矩阵表示为：X=,其中，矢量X的四个分量x1,x2,x3,x4满足如下条件：，试证明：这样的四维矢量X存在“无穷多个”，并可一般表示为：X=ax1+bx2+1/2 x3;其中x1=,x2=,x3=;而a,b为“任意实数”.

设A是n阶矩阵，且A的行列式|A|=0，则A中【】

已知α1=(1,0,2,3),α2=(1,1,3,5),α3=(1,-1,a+2,1),α4=(1,2,4,a+8)及β=(1,1,b+3,5).(1) a,b为何值时，β不能表示成α1,α2,α3,α4的线性组合？(2) a,b为何值时，β有α1,α2,α3,α4的唯一线性表示？并写出该表示式.

已知向量组α1,α2,α3,α4线性无关，则向量组【】

设α1=,α2=,α3=,α4=，若向量组α1,α2,α3与α1,α2,α4等价，则λ的取值范围是【】

设A是n×n实对称矩阵，证明：存在一个实数k使得对任意一个实n维向量x都有|x' Ax|≤kx'x，其中x'表示向量x的转置.

已知四维实矢量空间的矢量（表示成矩阵）：=,满足如下条件：以及T∙=9/4（其中，T表示对矩阵取置换），试求出所有这样的四维实矢量的集合：{ }=?

n维向量组α1,α2,…,αs (3≤s≤n)线性无关的充要条件是【】

已知向量α1=,α2=,β1=,β2=，若γ既可由α1,α2线性表示，也可由β1,β2线性表示，则γ=【】

向量组的线性相关性

设V是欧氏空间，W是V的子空间，V中的向量α不在W中，问是否存在α0∈W，使得α-α0与W的任意向量都正交？如果不存在，举出例子；如果存在，说明理由并讨论其唯一性.

设V是n维线性空间，φ为V上的线性变换，且φ的特征多项式为f(x)=(x-λ1 )m1(x-λ2 )m2(λ1≠λ2)其中m1+m2=n.(1)证明：Ker((φ-λ1 E)m1)是φ的不变子空间，其中E是恒等变换；(2)证明：V=Ker((φ-λ1 E)m1)⨁Ker((φ-λ2 E)m2).

设α1=(1,0,0,3),α2=(1,1,-1,2),α3=(1,2,a-3,1),α4=(1,2,-2,a),β=(0,1,b,-1)，问a,b为何值时(1) β能由α1,α2,α3,α4线性表示且表示唯一；(2) β不能由α1,α2,α3,α4线性表示；(3) β能由α1,α2,α3,α4线性表示但表示不唯一，并求一般表达式。

设α1,α2,…,αr是n维向量.令β1=α2+α3+⋯+αr,β2=α1+α3+⋯+αr,…,βr=α1+α2+⋯+αr-1.证明向量组β1,β2,…,βr与向量组α1,α2,…,αr有相同的秩.

设对角矩阵A的特征多项式为 φ(λ)=(λ-λi)ni （诸λi两两互异），求所有和A可交换的矩阵全体所组成的线性空间的维数.

用数学归纳法证明：对于复n维空间Vn上任意多个两两可交换的线性变换所组成的集合S具有公共的特征向量.

设R2中的内积为(α,β)=α' Aβ,A=，则,在此内积之下的度量矩阵为________.

已知同维数的两个向量组有相同的秩，且其中之一可用另外一个线性表示，证明：这两个向量组等价。

已知全体实的2维向量关于下列运算构成R上的线性空间V：(a1,b1 )+(a2,b2 )=(a1+a2,b1+b2+a1 a2),k∙(a,b)=(ka,kb+(k(k-1))/2 a2).(1)求V的一组基;(2)定义变换A(a,b)=(a,a+b)，证明：A是一个线性变换；并求A在V的一组基下的矩阵表示.

已知A ̅和B ̅分别是三维空间中的矢量矩阵和单位方向矢量;A ̅=Ax+Ay+Az;( Ax=,Ay=,Az=B ̅=cosα+cosβ+cosγ;( cos2 α+cos2 β+cos2 γ=1)计算矩阵求和c=k(A ̅∙B ̅)k +2k (A ̅∙B ̅)2k.提示：首先考察(A ̅∙B ̅)2=?