设非负函数f(x)在[0,+∞)上连续,给出以下三个命题:
①若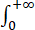 f² (x)收敛,则
f² (x)收敛,则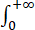 f(x)收敛.
f(x)收敛.
②若存在p>1,使得 xp f(x)存在,则
xp f(x)存在,则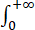 f(x)收敛.
f(x)收敛.
③若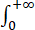 f(x)收敛,则存在p>1,使得
f(x)收敛,则存在p>1,使得 xp f(x)存在.
xp f(x)存在.
其中真命题个数为【 】
A、0
B、1
C、2
D、3
设非负函数f(x)在[0,+∞)上连续,给出以下三个命题:
①若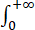 f² (x)收敛,则
f² (x)收敛,则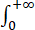 f(x)收敛.
f(x)收敛.
②若存在p>1,使得 xp f(x)存在,则
xp f(x)存在,则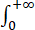 f(x)收敛.
f(x)收敛.
③若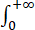 f(x)收敛,则存在p>1,使得
f(x)收敛,则存在p>1,使得 xp f(x)存在.
xp f(x)存在.
其中真命题个数为【 】
A、0
B、1
C、2
D、3
B
【解析】
解答过程见word版
证明:当x>0时,ln√x=1/(2n-1) ((x-1)/(1+x))2n-1 ,并讨论1/(2n-1) ((x-1)/(1+x))2n-1关于x∈(0,+∞)是否一致收敛.
级数n!/nn e-n-x的收敛域为(a,+∞),则a=________.
求证:(-1)n-1x2/(1+x2 )n 在R上一致收敛.
设函数项级数ne-nx ,x∈(0,+∞).(1)证明此级数在(0,+∞)上收敛但不一致收敛;(2)求此级数的和函数;(3)给出数项级数n/e3n 的和.
已知含参变量积分F(x)=sin(xy)/(ln(lny)) dy,证明:(1) F(x)在[δ,+∞)上关于x一致收敛(δ>0)(2) F(x)在(0,+∞)上关于x不一致收敛.
已知{un(x)}是可微函数列,且un(x)在[a,b]上一致有界,证明:若un(x)收敛,则un(x)必定一致收敛.
解答如下问题:(1)证明:(-1)n n(n+1)/(n(n+1) x2+2n)关于x∈(-∞,+∞)一致收敛.(2)计算(-1)n n(n+1)/(n(n+1) x2+2n ).
设数列{an}满足a1=1,(n+1) an+1=(n+1/2) an,证明:当|x|<1时,幂级数an xn 收敛,并求其和函数.
已知f(x)=,将f(x)展开成正弦级数,并求该级数的和函数.
设f(x)=(1)求f(x)的傅里叶级数与傅里叶级数的和函数;(2)证明:1/n2 =π2/6.
设级数sinnx/(1+nx2)(1)当x取何值时,级数绝对收敛?并说明理由;(2)当x取何值时,级数条件收敛?并说明理由.
已知an<bn (n=1,2,⋯), 若级数an ,与bn 均收敛,则“an 绝对收敛”是“bn 绝对收敛的”【 】
设f(x)为周期为2的周期函数,且f(x)=1-x,x∈[0,1],若f(x)=a0/2+ancosnπx,则a2n =________.
函数f(z)=1/(z-1)(z-2)在圆环区域:(1) 0<|z|<1;(2) 1<|z|<2;(3) 2<|z|<+∞;内是处处解析的。试把f(z)在这些区域内展成洛朗级数。
设f(x)是周期为2的周期函数,它在区间(-1,1]上定义为f(x)=,则f(x)的傅里叶级数在x=1处收敛于______.