设P=P(x,y,z),Q=Q(x,y,z)均为连续函数,Σ为曲面z=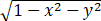 (x≤0,y≥0)的上侧,则∬ΣPdydz+Qdzdx=【 】
(x≤0,y≥0)的上侧,则∬ΣPdydz+Qdzdx=【 】
A、∬Σ(x/z P+y/z Q)dxdy
B、∬Σ(-x/z P+y/z Q)dxdy
C、∬Σ(x/z P-y/z Q)dxdy
D、∬Σ(-x/z P-y/z Q)dxdy
设P=P(x,y,z),Q=Q(x,y,z)均为连续函数,Σ为曲面z=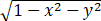 (x≤0,y≥0)的上侧,则∬ΣPdydz+Qdzdx=【 】
(x≤0,y≥0)的上侧,则∬ΣPdydz+Qdzdx=【 】
A、∬Σ(x/z P+y/z Q)dxdy
B、∬Σ(-x/z P+y/z Q)dxdy
C、∬Σ(x/z P-y/z Q)dxdy
D、∬Σ(-x/z P-y/z Q)dxdy
A
【解析】
解答过程见word版
设函数f(x)=ecostdt,g(x)=et² dt,则【 】
设函数f(x)=sint3dt,g(x)=f(t)dt,则【 】
设函数y=f(x)由参数方程确定,则x[f(2+2/x)-f(2)]=【 】
函数f(x)=|x|1/(1-x)(x-2)的第一类间断点的个数是【 】
证明双曲抛物面同族的任意两条直母线必是异面直线,且同族的全体直母线平行于同一个平面.
在直角坐标系下,已知一点M0 (1,2,0)和一条直线L:,求M0到L的距离,并写出过M0且与L垂直相交的直线方程.
设V是欧氏空间,W是V的子空间,V中的向量α不在W中,问是否存在α0∈W,使得α-α0与W的任意向量都正交?如果不存在,举出例子;如果存在,说明理由并讨论其唯一性.
设Σ为曲面z=(1≤x²+y²≤4)的下侧,f(x)是连续函数,计算I=∬Σ(xf(xy)+2x-y)dydz+(yf(xy)+2y+x)dzdx+(zf(xy)+z)dxdy.
设平面有界区域D位于第一象限,由曲线xy=1/3,xy=3与直线y=1/3 x,y=3x围成,计算∬D(1+x-y)dxdy.
已知平面区域D={(x,y)|√(1-y²)≤x≤1,-1≤y≤1},计算∬Dx/√(x²+y²) dxdy.
计算曲面积分∬ΣzdS,其中Σ为锥面z=在柱体x2+y2≤2x内的部分.
计算曲面积分I=∬Σ (axdydz+(z+a)2dxdy)/(x2+y2+z2 )1/2 ,其中Σ为下半球面z=-的上侧,a为大于零的常数.
计算 ∬∑x3dydz,其中∑: x2/a2 +y2/b2 +z2/c2 =1,z≥0,取外侧.
已知S={(x,y,z)│x2+4y2+9z2=1,z≤0}取下侧,求∬S(yez+x)dydz+(zex+y)dzdx+(xcosxy+z)dxdy
已知S:(x-5)2+2y2+2(z+1)2=3,方向取外侧,计算∬S((x-5)dydz+ydzdx+zdxdy)/[(x-5)2+y2+z2 ](3/2)
设Σ为空间区域{(x,y,z)|x2 + 4y2≤4,0≤z≤2}表面的外侧,则曲面积分∬Σx2dydz + y2dzdx + z2dxdy=______.
设有界区域D是圆x2 + y2 = 1和直线y=x以及x轴在第一象限围成的部分,计算二重积分(x2 - y2)dxdy.
计算曲线积分I=∫(4x-y)/(4x²+y² ) dx+(x+y)/(4x²+y² ) dy,其中I是曲线L:x²+y²=2,方向为逆时针方向.
计算∫L(x²+y²+z²)ds,其中L:x=acost,y=asint,z=bt,t∈[0,2π].
计算∫Γex(1-cosy)dx-ex(y-siny)dy,其中Γ:y=sinx,x∈[0,π],方向从(π,0)到(0,0).
已知有向曲线L为球面x²+y²+z²=2x与平面2x-z-1=0交线,从z轴正向往z轴负向看去为逆时针方向,计算曲线积分∫L(6xyz-yz²)dx+2x²zdy+xyzdz.
计算∯Σ 2zxdydz+yzdzdx-z2 dxdy,其中Σ是由曲面z=与z=所围成的表面外侧.
计算曲面积分∬S(2x+z)dydz+zdxdy,其中S为有向曲面z=x2+y2 (0≤z≤1),其法向量与z轴正向的夹角为锐角.
计算曲线积分∮C(z-y)dx+(x-z)dy+(x-y)dz,其中C是曲线从z轴正向往z轴负向看,C的方向是顺时针的.
设L为椭圆x2/4+y2/3=1,其周长记为a,则∮L(2xy+3x2+4y2)ds=__________.
确定常数λ,使在右半平面x>0上的向量A(x,y)=2xy(x4+y2 )λ i-x2 (x4+y2 )λ j为某二元函数u(x,y)的梯度,并求u(x,y).
求I=∫L[exsiny-b(x+y)]dx+(excosy-ax)dy,其中a,b为常数,L为从点A(2a,0)沿曲线y=到点O(0,0)的弧.