大学数学-考研试题(理工数学Ⅰ 1999年对弧长的曲线积分)

问答题（1999年理工数学Ⅰ）

求I=∫_L[e^xsiny-b(x+y)]dx+(e^xcosy-ax)dy，其中a,b为常数，L为从点A(2a,0)沿曲线y=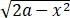到点O(0,0)的弧.

答案解析

被积表达式Pdx+Qdy=ex sinydx+ex cosydy-b(x+y)dx-axdy=d(ex siny)-b(x+y)dx-axdy,前一积分∫Lex sinydx+ex cosydy= ex siny=0,对后一积分∫Lb(x+y)dx+a...

查看完整答案

讨论

格林公式

设u∈C2 (R3)且∆u(x)=((∂2 u)/(∂x12 )+(∂2 u)/(∂x22 )+(∂2 u)/(∂x32 ))(x)=λu(x),λ为正常数，已知存在C>0，使得|x|≥C时，u≡0，求证：u(x)≡0,∀x∈R3.

计算∫Lxdy-ydx，其中L:x2+y2=1，取逆时针方向.

已知函数y=y(x)在任意点x处的增量Δy=yΔx/(1+x2)+α，且当Δx→0时，α是∆x(∆x→0)的高阶无穷小，y(0)=π，则y(1)等于【】

从船上向海中沉放某种探测仪器，按探测要求，需确定仪器的下沉深度y(从海平面算起)与下沉速度v之间的函数关系.设仪器在重力作用下，从海平面由静止开始铅直下沉，在下沉过程中还受到阻力和浮力的作用.设仪器的质量为m，体积为B，海水比重为ρ，仪器所受的阻力与下沉速度成正比，比例系数为k(k>0).试建立y与v所满足的微分方程，并求出函数关系式 y= y(v).

设A是n阶矩阵，若存在正整数k，使线性方程组Akx=0有解向量α，且Ak-1α≠0，证明向量组α,Aα,…,Ak-1α是线性无关的.

已知线性方程组(I)的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T，试写出线性方程组(II)有通解，并说明理由.

设某次考试的学生成绩服从正态分布，从中随机地抽取36位考生的成绩,算得平均成绩为66.5分，标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?并给出检验过程.附表：t分布表 P{t(n)≤t_p (n)}=p

设(X1,Y1 ),(X2,Y2 ),…,(Xn,Yn )为来自总体N(μ1,μ2;σ12,σ22;ρ)的简单随机样本. 令θ=μ1 - μ2, X ̅=1/n·Xi ,Y ̅=1/n·Yi ,θ ̂=X ̅ - Y ̅，则【】

甲乙两个盒子中各装有2个红球和2个白球，先从甲盒中任取一球，观察颜色后放入乙盒中，再从乙盒中任取一球.令X，Y分别表示从甲盒和乙盒中取到的红球个数，则X与Y的相关系数______.

已知曲线C:，求C上的点到xoy坐标面距离的最大值.

曲线积分与曲面积分

设F=yz(2x+y+z)i+xz(x+2y+z)j+xy(x+y+2z)k.求：F沿螺线r=acost∙i+asint∙j+bt∙k的一段（t:0→π/4）所作的功.

设曲面：z=z(x,y)=x4+1/2 (√5-4y)∙x2+y2，柱壁面：y=x2-5/9，圆柱体：x2+y2≤1，在三维空间O-XYZ中的“点的集合”分别为G1,G2,G3.(1)说明“点集”：G=G1∩G2∩G3构成了在三维空间O-XYZ中的有限长度的曲线L.(2)采用“参数方程”：，[t∈T；(T为参变数t的“取值集合”)]表示出曲线L.(3)计算曲线L的“总长度”：L=？提示：(i)选择参变数t=x,(ii)考虑柱壁面：y=x2-5/9与圆柱面：x2+y2=1满足相交或满足相切？[不定积分公式：∫dx=x/2 +a2/2 ln⁡(x+)+C可直接引用]

设曲面：z=z(x,y)=(y-x2)2+√5/2 x2，柱壁面：9y-9x2+5=0，圆柱体：x2+y2≤1，在三维空间O-XYZ中的“点的集合”分别为G1,G2,G3.(1)说明“点集”：G=G1∩G2∩G3构成了在三维空间O-XYZ中的有限长度的曲线L.(2)采用“参数方程”：，[t∈T；(T为参变数t的“取值集合”)]表示出曲线L.(3)计算曲线L的“总长度”：L=？提示：(i)选择参变数t=x,(ii)考虑柱壁面：y=x2-5/9与圆柱面：x2+y2=1满足相交或满足相切？[不定积分公式：∫dx=x/2 +a2/2 ln⁡(x+)+C可直接引用]

设L为取正向的圆周x2+y2=9，则曲线积分∮L(2xy-2y)dx+(x2 - 4x)dy=________.

计算曲面积分I=∬∑x(8y+1)dydz+2(1-y2 )dxdz-4yzdxdy,其中∑是由曲线(1≤y≤3)绕y轴旋转一周而成的曲面，其法向量与y轴正向的夹角恒大于π/2.

设平面L是下半圆周y=-，则曲线积分∫L(x2+y2)ds=________.

向量场u(x,y,z)=xy2i+ye2j+xln(1+z2)k在点P(1,1,0)处的散度divu=________.

设曲线积分∫Cxy2dx+yφ(x)dy与路径无关，其中φ(x)具有连续的导数，且φ(0)=0，计算xy2dx+yφ(x)dy的值.

求曲面积分I=∬S yzdzdx+2dxdy，其中S是球面x2+y2+z2=4外侧在z≥0的部分.

质点P沿着以AB为直径的半圆周，从点A(1,2)运动到点B(3,4)的过程中受变力F作用(见图).F的大小等于点P与原点O之间的距离，其方向垂直于线段OP且与y轴正向的夹角小于π/2求变力F对质点P所做的功.

对弧长的曲线积分

在过点O(0,0)和A(π,0)的曲线族y=asinx(a>0)中，求一条曲线L，使沿该曲线从O到A的积分∫L(1+y3) dx+(2x+y)dy的值最小.

在变力F=yzi+zxj+xyk的作用下，质点由原点沿直线运动到椭球面x2/a2 +y2/b2 +z2/c2 =1上第一卦限的点M(ξ,η,ζ)，问当ξ,η,ζ取何值时，力F所做的功W最大？并求出W的最大值.

设曲线积分∫L[f(x)-ex]sinydx-f(x)cosydy与路径无关，共中f(x)具有一阶连续导数，且f(0)=0，则f(x)等于【】

设函数Q(x,y)在xOy平面上具有一阶连续偏导数，曲线积分∫L2xydx+Q(x,y)dy与路径无关，并且对任意t恒有2xydx+Q(x,y)dy=2xydx+Q(x,y)dy，求Q(x,y).

计算曲线积分∮C(z-y)dx+(x-z)dy+(x-y)dz，其中C是曲线从z轴正向往z轴负向看，C的方向是顺时针的.

设L为椭圆x2/4+y2/3=1，其周长记为a，则∮L(2xy+3x2+4y2)ds=__________.

设D⊂R2是有界单连通闭区域，I(D)=(4-x2-y2)dxdy取得最大值的积分区域记为D1.(1) 求I(D1 )的值.(2) 计算，其中∂D1是D1的正向边界.

设Γ是上半球面x2+y2+z2=R2 (z≥0)上的光滑曲线，起点和终点分别在平面z=0,z=R/2上，曲线的切线与z轴正方向的夹角为常数α∈(0,π/6)，求曲线Γ的长度.

计算积分x3 J0 (x)dx

计算积分∬SzdS，其中S为曲面x2+z2=2az(a>0)被曲面z=所截的部分.