设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生的成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?并给出检验过程.
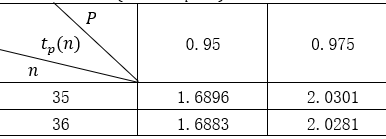
附表:t分布表 P{t(n)≤t_p (n)}=p
设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生的成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?并给出检验过程.
附表:t分布表 P{t(n)≤t_p (n)}=p

设该次考试全体考生的成绩为总体X,则X~N(μ,σ2 ),σ2未知.把从X中抽取的容量为n的样本均值记为X ̅,样本标准差记为s,在显著性水平α=0.05下检验假设:H0:μ=70;H1:μ≠70,选取检验统计量 T=~t(n-1),则拒绝域为:|t|=≥t_(1-α/2) (...
查看完整答案设两个随机变量X、Y相互独立,且都服从均值为0、方差为1/2的正态分布,求随机变量|X-Y|的方差.
已知线性方程组(I)的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T,试写出线性方程组(II)有通解,并说明理由.
设A是n阶矩阵,若存在正整数k,使线性方程组Akx=0有解向量α,且Ak-1α≠0,证明向量组α,Aα,…,Ak-1α是线性无关的.
已知二次曲面方程x2+ay2+z2+2bxy+2xz+2yz=4,可以经过正交变换=P化为椭圆柱面方程η2+4ζ2=4,求a,b的值和正交矩阵P.
设正向数列{an}单调减少,且(-1)nan 发散,试问级数(1/(an+1))n 是否收敛?并说明理由.
求[sin(π/n)/(n+1)+sin(2π/n)/(n+1/2)+⋯+sinπ/(n+1/n)]
计算曲面积分I=∬Σ (axdydz+(z+a)2dxdy)/(x2+y2+z2 )1/2 ,其中Σ为下半球面z=-的上侧,a为大于零的常数.
设f(x)具有二阶连续导数,f(0)=0,f'(0)=1,且[xy(x+y)-f(x)y]dx+[f'(x)+x2y]dy=0为一阶全微分方程,求f(x)及此全微分方程的通解.
已知点A与B的直角坐标分别为(1,0,0)与(0,1,1).线段AB绕z轴旋转一周所成的旋转曲面为S.求由S及两平面z=0,z=1所围成的立体体积.
设曲线l位于xOy平面的第一象限内,l上任一点M处的切线与y轴总相交,交点记为A.已知||=||,且l过点(3/2,3/2),求l的方程.
设工厂A 和工厂B的产品的次品率分别为1% 和 2%,现从由 A 厂和 B厂的产品分别占60% 和 40% 的一批产品中随机抽取一件,发现是次品,则该次品属 A厂生产的概率是________.
袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第2个人取行得黄球的概率是________.
设α1=,α2=,α3=,则三条直线a1 x+b1 y+c1=0,a2 x+b2 y+c2=0,a3 x+b3 y+c3=0,(其中ai2+bi2≠0,i=1,2,3)相交于一点的充要条件是【 】
设总体X的概率密度为f(x)=,其中θ>-1是未知参数.X1,X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.
设A,B是两个随机事件,且0<P(A)<1,P(B│A)=P(B|A ̅),则必有【 】
求直线l:(x-1)/1=y/1=(z-1)/-1在平面π:x-y+2z-1=0上的投影直线l0的方程,并求l0绕y轴旋转一周所成曲面的方程.
二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【 】
设A,B为随机事件,且0<P(B)<1,下列命题中为假命题的是【 】
欧拉方程x2y″ + xy' - 4y = 0满足条件y(1) = 1,y'(1) = 2得解为y = ______.
在区间(0,2)上随机取一点,将该区间分成两段,较短的一段长度记为X,较长的一段记为Y,令Z=Y/X.(1) 求X的概率密度;(2) 求Z的概率密度;(3) 求E(X/Y).