从正态总体N(3.4,62)抽取容量为n的样本,如果要求其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n至少应取多大?
附表:标准正态分布表Φ(z)=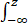
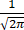
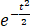 dt.
dt.
z 1.28 1.645 1.96 2.33
Φ(z) 0.900 0.950 0.975 0.990
从正态总体N(3.4,62)抽取容量为n的样本,如果要求其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n至少应取多大?
附表:标准正态分布表Φ(z)=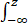
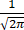
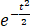 dt.
dt.
z 1.28 1.645 1.96 2.33
Φ(z) 0.900 0.950 0.975 0.990
以X ̅表示样本均值,因X~N(3.4,62),于是(X ̅-3.4)/(6/√n)~N(0,1),则P{1.4<X ̅<5.4}=P{<<} =Φ(√n/3)-Φ(-√n...
查看完整答案设两个随机变量X、Y相互独立,且都服从均值为0、方差为1/2的正态分布,求随机变量|X-Y|的方差.
已知线性方程组(I)的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T,试写出线性方程组(II)有通解,并说明理由.
设A是n阶矩阵,若存在正整数k,使线性方程组Akx=0有解向量α,且Ak-1α≠0,证明向量组α,Aα,…,Ak-1α是线性无关的.
已知二次曲面方程x2+ay2+z2+2bxy+2xz+2yz=4,可以经过正交变换=P化为椭圆柱面方程η2+4ζ2=4,求a,b的值和正交矩阵P.
设正向数列{an}单调减少,且(-1)nan 发散,试问级数(1/(an+1))n 是否收敛?并说明理由.
求[sin(π/n)/(n+1)+sin(2π/n)/(n+1/2)+⋯+sinπ/(n+1/n)]
计算曲面积分I=∬Σ (axdydz+(z+a)2dxdy)/(x2+y2+z2 )1/2 ,其中Σ为下半球面z=-的上侧,a为大于零的常数.
确定常数λ,使在右半平面x>0上的向量A(x,y)=2xy(x4+y2 )λ i-x2 (x4+y2 )λ j为某二元函数u(x,y)的梯度,并求u(x,y).
设某产品寿命服从正态分布即Z ~ N(10,22)分布,试求任取5件中恰有2件寿命超过产品期望寿命的概率。
若随机变量X服从参数λ=1的指数分布,则P(-2<x<2)=__________。
设随机变量X~U(0,3),随机变量Y服从参数为2的泊松分布,且X与Y的协方差为-1,则D(2X-Y+1)=【 】
求微分方程y'''+6y''+(9+a2) y'=1的通解,其中常数a>0.
问a,b为何值时,线性方程组有唯一解?无解?有无穷解?并求出有无穷解时的通解.
设在一次试验中,事件A发生的概率为p,现进行n次独立试验,则A至少发生一次的概率为__________;而事件A至多发生一次的概率为__________.
设随机变量X的概率密度函数为fX(x)=1/(π(1+x2)),求随机变量Y=1-∛X的概率密度函数fY(y).
设矩阵A=,E=,则逆矩阵(A-2E)-1=________.
已知随机事件A的概率P(A)=0.5,随机事件B的概率P(B)=0.6以及条件概率P(B|A)=0.8,则和事件A∪B的概率P(A∪B)=______.
甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为______.
随机变量ξ在(1,6)上服从均匀分布,则方程x2+ξx+1=0有实根的概率是______.
设f(x)=sinx-(x-t)f(t)dt,其中f为连续函数,求f(x).
设随机变量X与Y独立,且X服从均值为1、标准差(均方差)为√2的正态分布,而Y服从标准正态分布,试求随机变量Z=2X-Y+3的概率密度函数.