投保人的损失事件发生时,保险公司的赔付额Y与投保人的损失额X的关系为

Y=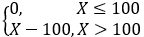

设损失事件发生时，投保人的损失额X的概率密度为

f(x)=

(1)求P{Y>0}及E(Y).

(2)这种损失事件在一年内发生的次数记为N，保险公司在一年内就这种损失事件产生的理赔次数记为M，假设N服从参数为8的泊松分布，在N=n(n≥1)的条件下，M服从二项分布B(n,P)，其中P=P{Y>0},求M的概率分布.

设X₁,X₂,⋯,X₂₀是来自总体B(1,0,1)的简单随机样本，令T=∑_i=1²⁰X_i ，利用泊松分布近似表示二项分布的方法可得P{T≤1}≈【 】

A、1/e²

B、2/e²

C、3/e²

D、4/e²

设二维随机变量(X,Y)服从正态分布N(0,0;1,1,ρ)，其中ρ∈(-1,1)，若a,b为满足a²+b²=1的任意实数，则D(aX+bY)的最大值为【 】

A、1

B、2

C、1+|ρ|

D、1+ρ²

随机变量X,Y相互独立，其X~N(0,2),Y~N(-1,1)，记p1={2X>Y},p2={X-2Y>1}，则【 】

A、p1>p2>1/2

B、p2>p1>1/2

C、p1<p2<1/2

D、p2<p1<1/2

设随机变量X,Y相互独立，且均服从参数为λ的指数分布，令Z=|X-Y|，则下列随机变量与Z同分布的是【 】

A、X-Y

B、(X+Y)/2

C、2X

D、X