投保人的损失事件发生时,保险公司的赔付额Y与投保人的损失额X的关系为
Y=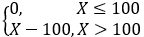
设损失事件发生时,投保人的损失额X的概率密度为
f(x)=
(1)求P{Y>0}及E(Y).
(2)这种损失事件在一年内发生的次数记为N,保险公司在一年内就这种损失事件产生的理赔次数记为M,假设N服从参数为8的泊松分布,在N=n(n≥1)的条件下,M服从二项分布B(n,P),其中P=P{Y>0},求M的概率分布.
投保人的损失事件发生时,保险公司的赔付额Y与投保人的损失额X的关系为
Y=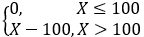
设损失事件发生时,投保人的损失额X的概率密度为
f(x)=
(1)求P{Y>0}及E(Y).
(2)这种损失事件在一年内发生的次数记为N,保险公司在一年内就这种损失事件产生的理赔次数记为M,假设N服从参数为8的泊松分布,在N=n(n≥1)的条件下,M服从二项分布B(n,P),其中P=P{Y>0},求M的概率分布.
解答过程见word版
设矩阵A=,已知1是A的特征多项式的重根.(1)求a的值;(2)求所有满足Aα=α+β,A²α=α+2β的非零列向量α,β.
设Σ是由直线 绕直线 (t为参数)旋转一周得到的曲面,Σ1是Σ介于平面x+y+z=0与x+y+z=1之间部分的外侧,计算曲面积分∬Σ1xdydz+(y+1)dzdx+(z+2)dxdy.
设A,B为两个不同随机事件,且相互独立,已知P(A)=2P(B),P(A∪B)=5/8,则A,B中至少有一个发生的条件下,A,B中恰好有一个发生的概率为______.
设矩阵A=,若方程组A²X=0与AX=0不同解,则a-b=______.
已知有向曲线L是沿抛物线y=1-x²从点A(1,0)到B(-1,0)的一段,则曲线积分∫L(y+cosx)dx+(2x+cosy)dy=______.
已知函数v(x,y,z)=xy²z³,向量n→=(2,2,-1),则 ∂v/(∂n)|(1,1,1)=______.
已知函数f(x)=的傅里叶级数为bn sinnπx,S(x)为bn sinnπx的和函数,则S(-7/2)=______.
设X1,X2,⋯,X100为来自总体X的简单随机样本,其中P{X=0}=P{X=1}=1/2,Φ(x)表示标准正态分布函数,则利用中心极限定理可得P{Xi≤55}的近似值为【 】
设随机变量X,Y相互独立,且X服从正态分布N(0,2),Y服从正态分布N(-2,2),若P{2X+Y<a}=P{X>Y},则a=【 】
设随机变量X,Y相互独立,且均服从参数为λ的指数分布,令Z=|X-Y|,则下列随机变量与Z同分布的是【 】
随机变量X,Y相互独立,其X~N(0,2),Y~N(-1,1),记p1={2X>Y},p2={X-2Y>1},则【 】
设二维随机变量(X,Y)服从正态分布N(0,0;1,1,ρ),其中ρ∈(-1,1),若a,b为满足a²+b²=1的任意实数,则D(aX+bY)的最大值为【 】
设X1,X2,⋯,X20是来自总体B(1,0,1)的简单随机样本,令T=∑i=120Xi ,利用泊松分布近似表示二项分布的方法可得P{T≤1}≈【 】
总体X的均匀分布为F(X),X1,X2,⋯,Xn为来自总体X的简单随机样本,样本的经验分布函数为Fn(x),对于给定的x(0<F(x)<1),D(F(x))=【 】