设矩阵A=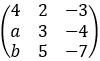
，若方程组A²X=0与AX=0不同解，则a-b=______.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设矩阵A=,β=，已知线性方程组AX=β有解但不唯一.(1)求a的值；(2)求一个正交矩阵Q，使得QTAQ为对角矩阵.
已知数列{xn },{yn },{zn}满足x0=-1,y0=0,z0=2，且，记αn=，写出满足αn=Aαn-1的矩阵A，并求An及xn,yn,zn.
求线性方程组的基础解系，假设该方程组的一个解和另外一个解为k1+k2 的方程组有公共解，求出所有公共解.
对方程组，试问用Jacobi迭代和Gauss-Seidel迭代是否收敛？为什么？
已知线性方程组(I)的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T，试写出线性方程组(II)有通解，并说明理由.
设二次型f(x1,x2 )=x1²-4x1 x2+4x2²经正交变换=Q化为二次型g(y1,y2 )=ay1²+4y1 y2+by2²，其中a≥b.(1)求a,b的值；(2)求正交矩阵Q.
证明：秩等于r的矩阵可以表示为r个秩等于1的矩阵之和，但不能表示为少于r个秩等于1的矩阵之和.
设A是n阶满秩矩阵，证明：存在正交矩阵P1,P2使得P1-1AP2=其中λi>0(i=1,2,⋯,n).
设A为4阶矩阵，A*为A的伴随矩阵，若A(A-A*)=0，且A≠A*，则r(A)取值为【 】
设A是秩为2的3阶矩阵，α是满足Aα=0的非零向量，若对满足βTα=0的3维向量β均有Aβ=β，则【 】
设矩阵A=,B=，向量α=,β=.(1)证明：方程组Ax=α的解均为方程组Bx=β的解；(2)若方程组Ax=α与方程组Bx=β不同解，求a的值.
设A是5×4矩阵，且r(A)=3,β为5维非零向量，已知γ1,γ2,γ3为方程AX=β的3个不同的解，且γ1+γ2=(2,2,0,2)T,γ1+γ3=(0,0,2,0)T.求AX=β的通解.
设3阶矩阵A=(α1,α2,α3)，B=(β1,β2,β3)，若向量组α1,α2,α3可以由向量组β1,β2线性表出，则【 】
设A=(α1,α2,α3,α4)为4阶正交矩阵，若矩阵A = ,β = ,k表示任意常数，则线性方程组Ax=β的通解为x=【 】
设线性方程组Ax=b的系数矩阵A=。(1)试求能使Jacobi迭代法收敛的a的取值范围；(2)对该方程组写出Jacobi迭代格式（设b=(b1,b2,b3)T已知）。
设f(x)=，则f(x)=0的根为____________.
设A为n阶方阵，A*为A的伴随矩阵且A11≠0,b≠0，其中A11为A的a11对应的代数余子式.证明：AX=b有无穷多个解⟺b是A* X=0的解.