设线性方程组Ax=b的系数矩阵A=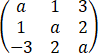 。
。
(1)试求能使Jacobi迭代法收敛的a的取值范围;
(2)对该方程组写出Jacobi迭代格式(设b=(b1,b2,b3)T已知)。
设线性方程组Ax=b的系数矩阵A=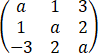 。
。
(1)试求能使Jacobi迭代法收敛的a的取值范围;
(2)对该方程组写出Jacobi迭代格式(设b=(b1,b2,b3)T已知)。
(1)若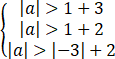 ,则A为严格对角占优的,是Jacobi迭代法收敛,
,则A为严格对角占优的,是Jacobi迭代法收敛,
解得:|a|>5.
(2)Jacobi迭代格式:
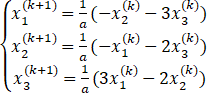 ,k=0,1,…;x(0)任取。
,k=0,1,…;x(0)任取。
设x0,x1,…,xn为n+1个互异的插值节点,li (x)(i=0,1,…,n)为拉格朗日基本插值多项式(也称为插值基本函数)。证明:(1) li (x)≡1;(2) li (x)xik≡xk.
若x=(-1,2,3,0,4),求‖x‖1,‖x‖2,‖x‖∞.
设Γ是上半球面x2+y2+z2=R2 (z≥0)上的光滑曲线,起点和终点分别在平面z=0,z=R/2上,曲线的切线与z轴正方向的夹角为常数α∈(0,π/6),求曲线Γ的长度.
若f(x):(0,π)→R连续,f(x)>0,f(π/2)=1,且对于任意的x∈(0,π)满足dt/(f2(t))=-cosx/(f(x)),求f(x)的表达式.
一卡车沙子通过传送带卸货,假设沙子落到地上堆成一个正圆锥体,且圆锥体的底面半径始终等于圆锥体的高,如果传送带以每分钟3立方米匀速卸沙,问当圆锥达到3米高时,卸了多少时间,此时圆锥高h的增长速度为多少?
设A=(α1,α2,α3,α4)为4阶正交矩阵,若矩阵A = ,β = ,k表示任意常数,则线性方程组Ax=β的通解为x=【 】
已知线性方程组(I)的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T,试写出线性方程组(II)有通解,并说明理由.
设A,B为n阶矩阵,E为单位矩阵.若方程组Ax=0与Bx=0同解,则【 】
设3阶矩阵A=(α1,α2,α3),B=(β1,β2,β3),若向量组α1,α2,α3可以由向量组β1,β2线性表出,则【 】
要使ξ1=,ξ2=都是方程组Ax=0的解,只要系数矩阵A为【 】
设n阶矩阵A的各行元素之和均为零,且A的秩为n-1,则线性方程组Ax=0的通解为____________.
设A为n阶方阵,A*为A的伴随矩阵且A11≠0,b≠0,其中A11为A的a11对应的代数余子式.证明:AX=b有无穷多个解⟺b是A* X=0的解.
设f(x)=,则f(x)=0的根为____________.
当λ,μ为何值时,方程组有惟一解?无解?有无穷解?无穷解时并求其全解.
设X1=(0 2 0)T,X2=(-3 3 2)T是方程组的两个解,求此方程组的一般解。
已知方程组I:,方程组II:问a,b为何值时方程组I和方程组II有相同的解?并求此相同解。
对方程组,试问用Jacobi迭代和Gauss-Seidel迭代是否收敛?为什么?
设x1-x2=a1,x2-x3=a2,x3-x4=a3,x4-x5=a4,x5-x1=a5。证明此方程组有解的充分必要条件为ai =0。
已知β1,β2是非齐次线性方程组Ax=b的两个不同的解,α1,α2是对应齐次线性方程组Ax=0的基础解系,k1,k2为任意常数,则方程组Ax=b的通解(一般解)必是【 】