大学数学-考研试题(重庆大学 2005年非齐次线性方程组)

问答题（2005年重庆大学）

当λ,μ为何值时，方程组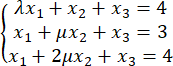有惟一解？无解？有无穷解？无穷解时并求其全解.

答案解析

暂无答案

讨论

大学数学

重庆大学克拉默法则

已知A ̅和B ̅分别是三维空间中的矢量矩阵和单位方向矢量;A ̅=Ax+Ay+Az;( Ax=,Ay=,Az=B ̅=cosα+cosβ+cosγ;( cos2 α+cos2 β+cos2 γ=1)计算矩阵求和c=k(A ̅∙B ̅)k +2k (A ̅∙B ̅)2k.提示：首先考察(A ̅∙B ̅)2=?

四维矢量X采用列矩阵表示为：X=,其中，矢量X的四个分量x1,x2,x3,x4满足如下条件：，试证明：这样的四维矢量X存在“无穷多个”，并可一般表示为：X=ax1+bx2+1/2 x3;其中x1=,x2=,x3=;而a,b为“任意实数”.

设曲面：z=z(x,y)=(y-x2)2+√5/2 x2，柱壁面：9y-9x2+5=0，圆柱体：x2+y2≤1，在三维空间O-XYZ中的“点的集合”分别为G1,G2,G3.(1)说明“点集”：G=G1∩G2∩G3构成了在三维空间O-XYZ中的有限长度的曲线L.(2)采用“参数方程”：，[t∈T；(T为参变数t的“取值集合”)]表示出曲线L.(3)计算曲线L的“总长度”：L=？提示：(i)选择参变数t=x,(ii)考虑柱壁面：y=x2-5/9与圆柱面：x2+y2=1满足相交或满足相切？[不定积分公式：∫dx=x/2 +a2/2 ln⁡(x+)+C可直接引用]

计算二重积分：∬Dds其中，积分区域D为曲线y(x)=与直线y=0所围成的区域.提示：①首先考察曲线y=y(x)⟹F(x,y)=0为何种曲线，②然后采用“平面极坐标”方法作计算？

已知二元函数z=z(x,y)：z(x,y)=1/4[4(tgx+tgy)2 - 12tgx∙tgy - 3]，试求：二元函数z=z(x,y)在正方形区域：D ̅:-π/4≤x≤π/4,-π/4≤y≤π/4 里的最大值zmax=?和最小值zmin=?，并指出二元函数z=z(x,y)在闭区域D ̅里何点处取得最大值zmax和最小值zmin?

已知三个关于自变量x的函数：y=f(x),z=g(x),t=h(x)，其“函数关系”由如下“隐函数方程组”确定出： (1)确定出y,z,t关于x的单值、连续的函数关系式（解析式）：y=f(x)=?,z=g(x)=?,t=h(x)=?及其各函数的定义域{x}=?提示：求解函数方程以及求解其后问题时，令e10/3 - 1=2a，可便于计算分析处理。(2)求出函数y=f(x)的一阶导数：dy/dx=f' (x)=?及其可导区域{x}=?(3)给出函数y=f(x)的图像草图.提示：①首先，寻找出函数f(x)的三个“零点”：xk=?[其中，f(xk )=0;(k=1,2,3)],以及一阶导数函数f'(x)的两个“零点”：xl'=?[其中，f' (xl' )=0;(l=1,2)].②然后，考察函数f(x)的渐近性质.③最后，利用①②的结果，便可绘制出函数f(x)的图像草图[注意：“零点”方程f(xk )=0最终可化为关于xk的三次方程，可采用（分组分解法）因式分解后再作求解].

已知全体实的2维向量关于下列运算构成R上的线性空间V：(a1,b1 )+(a2,b2 )=(a1+a2,b1+b2+a1 a2),k∙(a,b)=(ka,kb+(k(k-1))/2 a2).(1)求V的一组基;(2)定义变换A(a,b)=(a,a+b)，证明：A是一个线性变换；并求A在V的一组基下的矩阵表示.

设C=，求C101.

设A=，B是三阶非零方阵，且AB=O，求a,b以及B的秩.

非齐次线性方程组

已知方程组I:，方程组II:问a,b为何值时方程组I和方程组II有相同的解？并求此相同解。

设X1=(0 2 0)T,X2=(-3 3 2)T是方程组的两个解，求此方程组的一般解。

设x1-x2=a1,x2-x3=a2,x3-x4=a3,x4-x5=a4,x5-x1=a5。证明此方程组有解的充分必要条件为ai =0。

用LU方法求解方程组.

用Gauss消去法和Gauss列主元消去法求解方程组

设A为m×n矩阵，非齐次线性方程组Ax ̅=β ̅有唯一解的充分必要条件为：______________.

设矩阵A=,b=，则线性方程组Ax=b解的情况为【】

已知β1,β2是非齐次线性方程组Ax=b的两个不同的解，α1,α2是对应齐次线性方程组Ax=0的基础解系，k1,k2为任意常数，则方程组Ax=b的通解（一般解）必是【】

问λ为何值时，线性方程组有解？并求出解的一般形式.

问a,b为何值时，线性方程组有唯一解？无解？有无穷解？并求出有无穷解时的通解.

线性方程组

设A=(α1,α2,α3,α4)为4阶正交矩阵，若矩阵A = ,β = ,k表示任意常数，则线性方程组Ax=β的通解为x=【】

设h(z)是关于自然变量z的多项式.考虑系数在多项式环C[z]中的关于y的三次方程y3-3zy+h(z)=0.(i)当h(z)=-z3-1时，找到此方程的至少一个一次多项式函数解.(ii)假设方程y3-3zy+h(z)=0有三个互不相等的整函数解y=f1(z),f2(z),f3(z)，则h(z)可以取哪些多项式？注：整函数指在整个复平面上解析的函数.

设线性方程组Ax=b的系数矩阵A=。(1)试求能使Jacobi迭代法收敛的a的取值范围；(2)对该方程组写出Jacobi迭代格式（设b=(b1,b2,b3)T已知）。

对方程组，试问用Jacobi迭代和Gauss-Seidel迭代是否收敛？为什么？

电子科技大学齐次线性方程组

设X1,X2是齐次线性方程组Ax=0的基础解系，Y1,Y2是非齐次线性方程组Ax=b的两个解，证明X=k1 (X1+X2 )+k2 (X1-X2 )+(3Y1-2Y2 ),k1,k2∈R是Ax=b的通解。

设f(x)=，则f(x)=0的根为____________.

设3阶矩阵A=(α1,α2,α3)，B=(β1,β2,β3)，若向量组α1,α2,α3可以由向量组β1,β2线性表出，则【】

设A=，B为3阶非零矩阵，且AB=0，则t=______.

已知线性方程组(I)的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T，试写出线性方程组(II)有通解，并说明理由.