考研2025年理工数学Ⅰ( )
设矩阵A=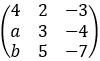 ,若方程组A²X=0与AX=0不同解,则a-b=______.
,若方程组A²X=0与AX=0不同解,则a-b=______.
-4
解答过程见word版
考研2025年理工数学Ⅰ( )
设α1,α2,α3,α4是n维向量,α1,α2线性无关,α1,α2,α3线性相关,且α1+α2+α4=0,在空间直角坐标系O-xyz中,关于x,y,z的方程组xα1+yα2+zα3=α4的几何图形是【 】
A、过原点的一个平面
B、过原点的一条直线
C、不过原点的一个平面
D、不过原点的一条直线
不过原点的一条直线
解答过程见word版
考研2024年高等代数( )
设A是5×4矩阵,且r(A)=3,β为5维非零向量,已知γ1,γ2,γ3为方程AX=β的3个不同的解,且γ1+γ2=(2,2,0,2)T,γ1+γ3=(0,0,2,0)T.求AX=β的通解.
考研2024年浙江大学( )
求线性方程组
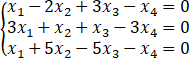
的基础解系,假设该方程组的一个解和另外一个解为k1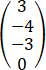 +k2
+k2 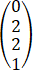 的方程组有公共解,求出所有公共解.
的方程组有公共解,求出所有公共解.
考研2024年经济数学Ⅲ( )
设矩阵A=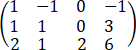 ,B=
,B=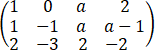 ,向量α=
,向量α=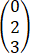 ,β=
,β=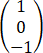 .
.
(1)证明:方程组Ax=α的解均为方程组Bx=β的解;
(2)若方程组Ax=α与方程组Bx=β不同解,求a的值.
解答过程见word版

