已知线性方程组
(I)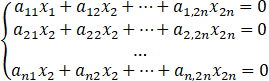
的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T,试写出线性方程组
(II)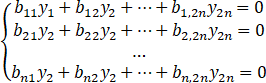
有通解,并说明理由.
已知线性方程组
(I)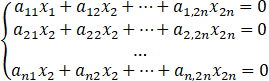
的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T,试写出线性方程组
(II)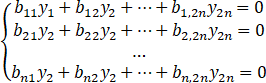
有通解,并说明理由.
(Ⅱ)的通解为y=C1(a11,a12,…,a1 2n)T+C2(a21,a22,…,a2 2n)T+⋯+Cn(an1,an2,…,an 2n)T,其中C1,C2,…,Cn为任意常数.理由:方程组(Ⅰ)、(Ⅱ)的系数矩阵分别记为A,B,则由题设可知ABT=0,于是BAT=ABT...
查看完整答案设A是n阶矩阵,若存在正整数k,使线性方程组Akx=0有解向量α,且Ak-1α≠0,证明向量组α,Aα,…,Ak-1α是线性无关的.
已知二次曲面方程x2+ay2+z2+2bxy+2xz+2yz=4,可以经过正交变换=P化为椭圆柱面方程η2+4ζ2=4,求a,b的值和正交矩阵P.
设正向数列{an}单调减少,且(-1)nan 发散,试问级数(1/(an+1))n 是否收敛?并说明理由.
求[sin(π/n)/(n+1)+sin(2π/n)/(n+1/2)+⋯+sinπ/(n+1/n)]
计算曲面积分I=∬Σ (axdydz+(z+a)2dxdy)/(x2+y2+z2 )1/2 ,其中Σ为下半球面z=-的上侧,a为大于零的常数.
确定常数λ,使在右半平面x>0上的向量A(x,y)=2xy(x4+y2 )λ i-x2 (x4+y2 )λ j为某二元函数u(x,y)的梯度,并求u(x,y).
求直线l:(x-1)/1=y/1=(z-1)/-1在平面π:x-y+2z-1=0上的投影直线l0的方程,并求l0绕y轴旋转一周所成曲面的方程.
设A=(α1,α2,α3,α4)为4阶正交矩阵,若矩阵A = ,β = ,k表示任意常数,则线性方程组Ax=β的通解为x=【 】
设线性方程组Ax=b的系数矩阵A=。(1)试求能使Jacobi迭代法收敛的a的取值范围;(2)对该方程组写出Jacobi迭代格式(设b=(b1,b2,b3)T已知)。
对方程组,试问用Jacobi迭代和Gauss-Seidel迭代是否收敛?为什么?
设f(x)=,则f(x)=0的根为____________.
设A为n阶方阵,A*为A的伴随矩阵且A11≠0,b≠0,其中A11为A的a11对应的代数余子式.证明:AX=b有无穷多个解⟺b是A* X=0的解.
设3阶矩阵A=(α1,α2,α3),B=(β1,β2,β3),若向量组α1,α2,α3可以由向量组β1,β2线性表出,则【 】