已知二次曲面方程x2+ay2+z2+2bxy+2xz+2yz=4,可以经过正交变换
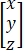 =P
=P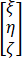
化为椭圆柱面方程η2+4ζ2=4,求a,b的值和正交矩阵P.
已知二次曲面方程x2+ay2+z2+2bxy+2xz+2yz=4,可以经过正交变换
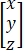 =P
=P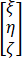
化为椭圆柱面方程η2+4ζ2=4,求a,b的值和正交矩阵P.
由题设知,矩阵A=与B=相似,于是有|λE-A|=|λE-B|,即=,解得a=3,b=1.此时A=,特征值为λ1=0,λ2=1,λ3=4.解(0E-A)x=0,得属于特征值λ1=0的特征向量为α1=(1,0,-1)T;解(E-A)x=0,得属于特征值λ2=1的特征向量为α2=(1,-1,1)T;解(4E-...
查看完整答案二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【 】
求一个正交变换,化二次型f=x12+4x22+4x32-4x1 x2+4x1 x3-8x2 x3成标准形.
已知二次型f(x1,x2,x3 )=2x12+3x22++3x32+2ax2 x3 (a>0)通过正交变换化成标准形f=y12+2y22+5y32,求参数a及所用的正交变换矩阵.
已知二次型f(x1,x2,x3 )=3x12+4x22+3x32+2x1 x3,(1)求正交变换x=Qy将f(x1,x2,x3)化为标准形;(2)证明minx≠0f(x)/(xT x)=2.
已知二次型f(x1,x2,x3 )=ijxixj.(1)求二次型矩阵.(2)求正交矩阵Q,使得二次型经正交变换x=Qy化为标准形.(3)求f(x1,x2,x3)=0的解.
二次型f(x1,x2,x3 )=(x1+x2 )2+(x1+x3 )2-4(x2-x3 )2的规范型为【 】
设A为n阶非零方阵,A*是A的伴随矩阵,AT的转置矩阵,当A*=AT时,证明|A|≠0.
设一平面经过原点及点P(6,-3,2),且与平面4x-y+2z=8垂直,则此平面方程为______________.
设A=E-ξξT,其中E是n阶单位矩阵,ξ是n维非零列向量,ξT是ξ的转置,证明:(1)A2=A的充要条件是ξTξ=1;(2)当ξTξ=1时,A是不可逆矩阵.
设A是n阶可逆方阵,将A的第i行和第j行对换后得到的矩阵记为B.(1)证明B可逆;(2)求AB-1.
设总体X的概率密度为f(x)=,其中θ>-1是未知参数.X1,X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.
已知α1=,α2=,α3=,记β1=α1,β2=α2 - kβ1,β3=α3 - l1 β1 - l2 β2,若β1,β2,β3 两两正交,则l1,l2依次为【 】
设A,B为随机事件,且0<P(B)<1,下列命题中为假命题的是【 】
欧拉方程x2y″ + xy' - 4y = 0满足条件y(1) = 1,y'(1) = 2得解为y = ______.
设A = aij为3阶矩阵,Aij为代数余子式,若A的每行元素之和均为2,且|A| = 3,A11 + A21 + A31 = ______.
在区间(0,2)上随机取一点,将该区间分成两段,较短的一段长度记为X,较长的一段记为Y,令Z=Y/X.(1) 求X的概率密度;(2) 求Z的概率密度;(3) 求E(X/Y).
与两直线及(x+1)/1=(y+2)/2=(z-1)/1都平行且过原点的平面方程为______________.
已知三维向量空间的基底为α1=(1,1,0)T,α2=(1,0,1)T,α3=(0,1,1)T,则向量β=(2,0,0)T在此基底下的坐标是____________.
设A为n阶方阵,且A的行列式|A|=a≠0,而A*是A的伴随矩阵,则|A* |等于【 】
已知连续随机变量X的概率密度函数为f(x)=,则X的数学期望为______;X的方差为______.
设4阶矩阵A=(α,γ2,γ3,γ4 ),B=(β,γ2,γ3,γ4),其中α,β,γ2,γ3,γ4均为四维列向量,且已知行列式|A|=4,|B|=1,则行列式|A+B|=________.