-
关注“优题吧”，分配平台账号.
题吧，智能辅助学习中心
考研2025年理工数学Ⅰ( )
二次型f(x1,x2,x3 )=x1²+2x1 x2+2x2 x3的正惯性指数为【 】
A、0
B、1
C、2
D、3
1
解答过程见word版
考研2024年高等代数( )
设n元实二次型f(x1,x2,⋯,xn )=l1²+⋯+ls²-ls+1²-ls+t²，其中li=ai1 x1+ai2 x2+⋯+ain xn,aij∈R,i=1,2,⋯,s+t,j=1,2,⋯,n.证明：f(x1,x2,⋯,xn )的正惯性指数p≤s.
考研2024年高等代数( )
设实矩阵
A=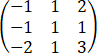
(1)求A的若尔当标准形J.
(2)求可逆矩阵P，使得P-1AP=J.
考研2024年高等代数( )
设复二次型
f(x1,x2,x3 )=2x1²+x2²-4x1 x2-4x2 x3
求非退化线性变换X=CY，将二次型f(x1,x2,x3 )化为规范形，其中X=(x1,x2,x3 )T,Y=(y1,y2,y3 )T，并写出规范形.
考研2024年浙江大学( )
已知矩阵
A=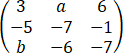
的特征值λ对应的特征向量α=
，求该矩阵的若当(Jordan)标准型.