已知二次型f(x1,x2,x3 )=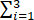
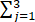 ijxixj.
ijxixj.
(1)求二次型矩阵.
(2)求正交矩阵Q,使得二次型经正交变换x=Qy化为标准形.
(3)求f(x1,x2,x3)=0的解.
已知二次型f(x1,x2,x3 )=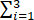
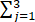 ijxixj.
ijxixj.
(1)求二次型矩阵.
(2)求正交矩阵Q,使得二次型经正交变换x=Qy化为标准形.
(3)求f(x1,x2,x3)=0的解.
(1) f(x1,x2,x3 )=ijxi xj=x12+4x22+9x32+4x1 x2+6x1 x3+12x2 x3,二次型矩阵为A=.(2) |λE-A|==λ2 (λ-14)=0,特征值为λ1=14,λ2=λ3=0.λ1=14时,(λE-A)=0的基础解系为α1=(1,2,3)T;λ2=λ3=0时,(λE-A)=0的基础解系为α2=(-2,1,0)T,α3=(-3,...
查看完整答案设函数f(x)在(-∞,+∞)上有二阶连续导数,证明:f'' (x)≥0的充要条件是:对任意不同的实数a,b,f((a+b)/2)≤1/(b-a)f(x)dx.
已知平面区域D={(x,y)|y-2≤x≤,0≤y≤2},计算I=∬D(x-y)2/(x2+y2)dxdy.
设y=y(x)满足y'+1/(2√x) y=2+√x,y(1)=3,求y(x)的渐近线.
设A,B,C满足:A,B互不相容,A,C互不相容,B,C相互独立,P(A)=P(B)=P(C)=1/3,则P[(B∪C)│(A∪B∪C) ]=__________.
设A,A-E可逆,若B满足(E-(A-E)-1 )B=A,则B-A=______________.
级数n!/nn e-n-x的收敛域为(a,+∞),则a=________.
二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【 】
求一个正交变换,化二次型f=x12+4x22+4x32-4x1 x2+4x1 x3-8x2 x3成标准形.
已知二次型f(x1,x2,x3 )=2x12+3x22++3x32+2ax2 x3 (a>0)通过正交变换化成标准形f=y12+2y22+5y32,求参数a及所用的正交变换矩阵.
已知二次曲面方程x2+ay2+z2+2bxy+2xz+2yz=4,可以经过正交变换=P化为椭圆柱面方程η2+4ζ2=4,求a,b的值和正交矩阵P.
已知二次型f(x1,x2,x3 )=3x12+4x22+3x32+2x1 x3,(1)求正交变换x=Qy将f(x1,x2,x3)化为标准形;(2)证明minx≠0f(x)/(xT x)=2.
二次型f(x1,x2,x3 )=(x1+x2 )2+(x1+x3 )2-4(x2-x3 )2的规范型为【 】
随机变量ξ在(1,6)上服从均匀分布,则方程x2+ξx+1=0有实根的概率是______.
设随机事件A,B及其和事件A∪B的概率分别是0.4,0.3,0.6,若B ̅表示B的对立事件,那么积事件AB ̅的概率P(AB ̅ )=________.
随机地向半圆0<y<(a为常数)内掷一点,点落在半圆内任何区域的概率与该区域的面积与正比,则原点和该点的连续与x轴的夹角小于π/4的概率为__________.
若连续函数f(x)满足关系式f(x)=f(t/2)dt+ln2,则f(x)等于【 】
微分方程y'+ytanx=cosx的通解为y=________________.
已知P(A)=P(B)=P(C)=1/4,P(AB)=0,P(AC)=P(BC)=1/6,则事件A,B,C全不发生的概率为__________.
设物体A从点(0,1)出发,以速度大小为常数v沿y轴正向运动,物体B从点(-1,0)与A同时出发,其速度大小为2v,方向始终指向A,试建立物体B的运动轨迹所满足的微分方程,并写出初始条件.
已知A,B两个事件满足条件P(AB)=P(A ̅B ̅),且P(A)=p,则P(B)=________.
设f(x)具有二阶连续导数,f(0)=0,f'(0)=1,且[xy(x+y)-f(x)y]dx+[f'(x)+x2y]dy=0为一阶全微分方程,求f(x)及此全微分方程的通解.
设曲线l位于xOy平面的第一象限内,l上任一点M处的切线与y轴总相交,交点记为A.已知||=||,且l过点(3/2,3/2),求l的方程.
设工厂A 和工厂B的产品的次品率分别为1% 和 2%,现从由 A 厂和 B厂的产品分别占60% 和 40% 的一批产品中随机抽取一件,发现是次品,则该次品属 A厂生产的概率是________.