已知平面区域D={(x,y)|y-2≤x≤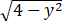
,0≤y≤2}，计算I=∬D(x-y)2/(x2+y2)dxdy.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（2022年理工数学Ⅰ；2022年理工数学Ⅱ；2022年经济数学Ⅲ）
答案解析
I=∬D(x-y)2/(x2+y2)dxdy=(cosθ-sinθ)2dθrdr+(cosθ-sinθ)2dθrdr=2(1-2sinθcosθ)dθ+2dθ=2(θ-sin2θ)+π=2(π/2-...
查看完整答案讨论
设y=y(x)满足y'+1/(2√x) y=2+√x,y(1)=3，求y(x)的渐近线.
设A,B,C满足：A,B互不相容，A,C互不相容，B,C相互独立，P(A)=P(B)=P(C)=1/3，则P[(B∪C)│(A∪B∪C) ]=__________.
设A,A-E可逆，若B满足(E-(A-E)-1 )B=A，则B-A=______________.
级数n!/nn e-n-x的收敛域为(a,+∞)，则a=________.
当x≥0,y≥0时，x2+y2≤kex+y恒成立，则k的最小值是__________.
函数f(x,y)=x2+2y2在(0,1)的最大方向导数为______.
设随机变量X~N(0,1)，在X=x条件下，随机变量Y~N(x,1)，则X与Y的相关系数为【 】
设随机变量X1,X2,…,Xn独立同分布，且X1的4阶矩阵存在.设μk=E(X1k)(k=1,2,3,4)，则由切比雪夫不等式，对∀ε>0，有P{|1/n Xi2 -μ2 |≥ϵ}≤【 】
计算曲面积分∬S(xdydz+z2dxdy)/(x2+y2+z2 )，其中S是由曲面x2+y2=R2及平面z=R,z=-R(R>0)所围成的立体表面的外侧.
计算曲面积分∬ΣzdS，其中Σ为锥面z=在柱体x2+y2≤2x内的部分.
计算曲面积分I=∬Σ (axdydz+(z+a)2dxdy)/(x2+y2+z2 )1/2 ，其中Σ为下半球面z=-的上侧，a为大于零的常数.
设S为椭球面x2/2+y2/2+z2=1的上半部分，点P(x,y,z)∈S,π为S在P处的切平面，ρ(x,y,z)为点O(0,0,0)到平面π的距离，求∬Sz/(ρ(x,y,z)) dS.
设Σ为空间区域{(x,y,z)|x2 + 4y2≤4,0≤z≤2}表面的外侧，则曲面积分∬Σx2dydz + y2dzdx + z2dxdy=______.
f(x)满足∫f(x)/dx = 1/6·x2 - x + C,L为曲线y=f(x)(4≤x≤9),L的弧长为s,L绕x轴旋转一周所形成的曲面的面积为A，求s和A.
曲线(x2 + y2)2 = x2 - y2 (x≥0,y≥0)与x轴围成的区域为D，求xydxdy.
设有界区域D是圆x2 + y2 = 1和直线y=x以及x轴在第一象限围成的部分，计算二重积分(x2 - y2)dxdy.
设曲线积分∫Cxy2dx+yφ(x)dy与路径无关，其中φ(x)具有连续的导数，且φ(0)=0，计算xy2dx+yφ(x)dy的值.
设数量场u=ln，则div(gradu)=________________.
确定常数λ，使在右半平面x>0上的向量A(x,y)=2xy(x4+y2 )λ i-x2 (x4+y2 )λ j为某二元函数u(x,y)的梯度，并求u(x,y).
计算曲面积分I=∬∑x(8y+1)dydz+2(1-y2 )dxdz-4yzdxdy,其中∑是由曲线(1≤y≤3)绕y轴旋转一周而成的曲面，其法向量与y轴正向的夹角恒大于π/2.
求曲面积分I=∬S yzdzdx+2dxdy，其中S是球面x2+y2+z2=4外侧在z≥0的部分.
在过点O(0,0)和A(π,0)的曲线族y=asinx(a>0)中，求一条曲线L，使沿该曲线从O到A的积分∫L(1+y3) dx+(2x+y)dy的值最小.
设曲线积分∫L[f(x)-ex]sinydx-f(x)cosydy与路径无关，共中f(x)具有一阶连续导数，且f(0)=0，则f(x)等于【 】
设函数Q(x,y)在xOy平面上具有一阶连续偏导数，曲线积分∫L2xydx+Q(x,y)dy与路径无关，并且对任意t恒有2xydx+Q(x,y)dy=2xydx+Q(x,y)dy，求Q(x,y).