设A,B为n阶矩阵,E为单位矩阵.若方程组Ax=0与Bx=0同解,则【 】
A、方程组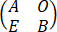 y=0只有零解
y=0只有零解
B、方程组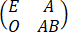 y=0只有零解
y=0只有零解
C、方程组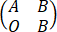 y=0与
y=0与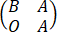 y=0同解
y=0同解
D、方程组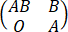 y=0与
y=0与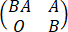 y=0同解
y=0同解
设A,B为n阶矩阵,E为单位矩阵.若方程组Ax=0与Bx=0同解,则【 】
A、方程组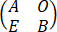 y=0只有零解
y=0只有零解
B、方程组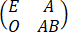 y=0只有零解
y=0只有零解
C、方程组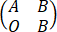 y=0与
y=0与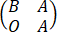 y=0同解
y=0同解
D、方程组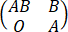 y=0与
y=0与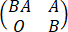 y=0同解
y=0同解
C
设A=(α1,α2,α3,α4)为4阶正交矩阵,若矩阵A = ,β = ,k表示任意常数,则线性方程组Ax=β的通解为x=【 】
设线性方程组Ax=b的系数矩阵A=。(1)试求能使Jacobi迭代法收敛的a的取值范围;(2)对该方程组写出Jacobi迭代格式(设b=(b1,b2,b3)T已知)。
对方程组,试问用Jacobi迭代和Gauss-Seidel迭代是否收敛?为什么?
设f(x)=,则f(x)=0的根为____________.
设A为n阶方阵,A*为A的伴随矩阵且A11≠0,b≠0,其中A11为A的a11对应的代数余子式.证明:AX=b有无穷多个解⟺b是A* X=0的解.
已知方程组I:,方程组II:问a,b为何值时方程组I和方程组II有相同的解?并求此相同解。
设X1=(0 2 0)T,X2=(-3 3 2)T是方程组的两个解,求此方程组的一般解。
设x1-x2=a1,x2-x3=a2,x3-x4=a3,x4-x5=a4,x5-x1=a5。证明此方程组有解的充分必要条件为ai =0。
设A为m×n矩阵,非齐次线性方程组Ax ̅=β ̅有唯一解的充分必要条件为:______________.
当λ,μ为何值时,方程组有惟一解?无解?有无穷解?无穷解时并求其全解.
问a,b为何值时,线性方程组有唯一解?无解?有无穷解?并求出有无穷解时的通解.
已知β1,β2是非齐次线性方程组Ax=b的两个不同的解,α1,α2是对应齐次线性方程组Ax=0的基础解系,k1,k2为任意常数,则方程组Ax=b的通解(一般解)必是【 】
已知矩阵A=,若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵,则P,Q可以分别取【 】
设A,B,C,D都是n×n矩阵,且|A|≠0,AC=CA,证明=|AD-CB|.
设A,B为n阶可逆矩阵,E为n阶单位矩阵,M*为M的伴随矩阵,则=【 】
设(a×b)∙c=2,则[(a+b)×(b+c)]∙(c+a)=________.
设A是n阶矩阵,满足AAT=E(E是n阶单位矩阵,AT是A的转置矩阵),|A|<0,求|A+E|.
微分方程y''-2y'+2y=ex的通解为____________.
设工厂A 和工厂B的产品的次品率分别为1% 和 2%,现从由 A 厂和 B厂的产品分别占60% 和 40% 的一批产品中随机抽取一件,发现是次品,则该次品属 A厂生产的概率是________.
设对任意x>0,曲线y=f(x)在点(x,f(x))处的切线在y轴上的截距等于1/x f(t)dt,求f(x)的一般表达式.