设a1=1,an=sinan-1 (n≥2)，证明：an≥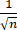
(n≥2).
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
已知函数f(x)是周期为π的奇函数，且当x∈（0，π/2）时f(x)=sinx-cosx+2，则当x∈（π，π/2）时f(x)=____________________.
函数y=sinx|sinx|（其中|x|≤π/2）的反函数为____________________.
设函数f(x)在[a,b]上有定义，在(a,b)上连续.下面哪个条件能够判定函数f(x)在[a,b]上有最大值【 】
设函数f(x)=，则函数f[f(x)]=__________.
能否用迭代法求下列方程，如不能，将方程改写为能用迭代法求解的形式.x=4-αx.
已知φ(x)=|x-t|f(t)dt，若积分存在，且f(x)>0，证明：φ(x)为[a,b]上的凸函数.
在平面直角坐标系中，椭圆x2+xy+y2=1的长轴方程为__________，位于x轴上半平面内的焦点坐标为__________.
设 f(x) 是连续函数，F(x)是 f(x)的原函数，则【 】
设f(x)=,f[φ(x)]=1-x，且φ(x)≥0，求φ(x)及其定义域.
f(x)=|xsinx| ecosx,-∞<x<+∞是【 】
若z=x+iy,f(z)=u(x,y)+iv(x,y)解析，且u-v=(x-y)(x2+4xy+y2)，求f(z).
求y=x3/(x-1)2 cos(2arctanx)的所有渐近线.
一卡车沙子通过传送带卸货，假设沙子落到地上堆成一个正圆锥体，且圆锥体的底面半径始终等于圆锥体的高，如果传送带以每分钟3立方米匀速卸沙，问当圆锥达到3米高时，卸了多少时间，此时圆锥高h的增长速度为多少？
计算(sin(x3y)+x2y)dxdy，其中D由y=x3,y=-1和x=1围成的有限闭区域.
设Γ是上半球面x2+y2+z2=R2 (z≥0)上的光滑曲线，起点和终点分别在平面z=0,z=R/2上，曲线的切线与z轴正方向的夹角为常数α∈(0,π/6)，求曲线Γ的长度.
若f(x):(0,π)→R连续，f(x)>0,f(π/2)=1，且对于任意的x∈(0,π)满足dt/(f2(t))=-cosx/(f(x))，求f(x)的表达式.
设a1=1,an=sinan-1 (n≥2)，证明：an≥(n≥2).
设a1=1,an=sinan-1 (n≥2)，证明：an≥(n≥2).
设a1=1,an=sinan-1 (n≥2)，证明：an≥(n≥2).
设a1=1,an=sinan-1 (n≥2)，证明：an≥(n≥2).
设a1=1,an=sinan-1 (n≥2)，证明：an≥(n≥2).