已知数列{xn },{yn },{zn}满足x0=-1,y0=0,z0=2，且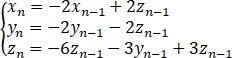
，记αn=
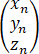，写出满足αn=Aαn-1的矩阵A，并求An及xn,yn,zn.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2024年理工数学Ⅰ）
答案解析
解答过程见word版
讨论
已知有向曲线L为球面x²+y²+z²=2x与平面2x-z-1=0交线，从z轴正向往z轴负向看去为逆时针方向，计算曲线积分∫L(6xyz-yz²)dx+2x²zdy+xyzdz.
已知平面区域D={(x,y)|√(1-y²)≤x≤1,-1≤y≤1}，计算∬Dx/√(x²+y²) dxdy.
设随机试验每次成功的概率为P，现进行3次独立重复试验，在至少成功1次的条件下，3次试验全部成功的概率为4/13，则P=______.
设实矩阵A=，若对任意实向量α=,β=,(αTAβ)²≤αTAα∙βTAβ都成立，则a的取值范围是________.
微分方程y'=1/(x+y)² 满足条件y(1)=0的解为__________.
已知函数f(x)=x+1，若f(x)=a0/2+ancosnx,x∈[0,π]，则n²sina2n-1 =______.
设函数f(u,v)具有2阶连续偏导数，且df|(1,1)=3du+4dv，令y=f(cosx,1+x²)，则d²y/dx²|x=0=______.
设矩阵A=,β=，已知线性方程组AX=β有解但不唯一.(1)求a的值；(2)求一个正交矩阵Q，使得QTAQ为对角矩阵.
已知线性方程组(I)的一个基础解系为(b11,b12,…,b1 2n)T,(b21,b22,…,b2 2n)T,…,(bn1,bn2,…,bn 2n)T，试写出线性方程组(II)有通解，并说明理由.
设A,B为n阶矩阵，E为单位矩阵.若方程组Ax=0与Bx=0同解，则【 】
要使ξ1=,ξ2=都是方程组Ax=0的解，只要系数矩阵A为【 】
设n阶矩阵A的各行元素之和均为零，且A的秩为n-1，则线性方程组Ax=0的通解为____________.
设A为n阶方阵，A*为A的伴随矩阵且A11≠0,b≠0，其中A11为A的a11对应的代数余子式.证明：AX=b有无穷多个解⟺b是A* X=0的解.
当λ,μ为何值时，方程组有惟一解？无解？有无穷解？无穷解时并求其全解.
设X1=(0 2 0)T,X2=(-3 3 2)T是方程组的两个解，求此方程组的一般解。
设A为m×n矩阵，非齐次线性方程组Ax ̅=β ̅有唯一解的充分必要条件为：______________.
问a,b为何值时，线性方程组有唯一解？无解？有无穷解？并求出有无穷解时的通解.
已知β1,β2是非齐次线性方程组Ax=b的两个不同的解，α1,α2是对应齐次线性方程组Ax=0的基础解系，k1,k2为任意常数，则方程组Ax=b的通解（一般解）必是【 】
设A=(α1,α2,α3,α4)为4阶正交矩阵，若矩阵A = ,β = ,k表示任意常数，则线性方程组Ax=β的通解为x=【 】