大学数学-考研试题(理工数学Ⅰ 2025年傅里叶级数)

填空题（2025年理工数学Ⅰ）

已知函数f(x)=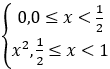的傅里叶级数为b_n sinnπx,S(x)为b_n sinnπx的和函数，则S(-7/2)=______.

答案解析

1/8

【解析】

解答过程见word版

讨论

大学数学

(xx-1)/(lnx∙ln⁡(1-x))=______.

设x1,x2,⋯,xn为来自总体N(μ,2)的简单随机样本，记X ̅=1/n xi ,Zα表示标准正态分布的上侧α分位数，假设检验问题：H0:μ≤1,H1:μ>1的显著性水平为α的检验的拒绝域为【】

设X1,X2,⋯,X20是来自总体B(1,0,1)的简单随机样本，令T=∑i=120Xi ，利用泊松分布近似表示二项分布的方法可得P{T≤1}≈【】

设二维随机变量(X,Y)服从正态分布N(0,0;1,1,ρ)，其中ρ∈(-1,1)，若a,b为满足a²+b²=1的任意实数，则D(aX+bY)的最大值为【】

设n阶矩阵A,B,C满足r(A)+r(B)+r(C)=r(ABC)+2n，给出下列四个结论：①r(ABC)+n=r(AB)+r(C);② r(AB)+n=r(A)+r(B);③ r(A)=r(B)=r(C)=n;④r(AB)=r(BC)=n，其中正确的选项是【】

设α1,α2,α3,α4是n维向量，α1,α2线性无关，α1,α2,α3线性相关，且α1+α2+α4=0，在空间直角坐标系O-xyz中，关于x,y,z的方程组xα1+yα2+zα3=α4的几何图形是【】

二次型f(x1,x2,x3 )=x1²+2x1 x2+2x2 x3的正惯性指数为【】

设函数f(x,y)连续，则dy=【】

设函数f(x)在区间[0,+∞)上可导，则【】

已知级数①sin⁡(n³ π)/(n²+1) ，②(-1)n(1/∛n² -tan⁡1/∛n²) ，则【】

傅里叶级数

设f(x)在(-∞,+∞)上可导，且对任意实数x有f(x)=f(x+2k)=f(x+b)，其中k为正整数，b为正无理数，用Fourier级数理论证明f(x)为常数.

设f(x)=(1)求f(x)的傅里叶级数与傅里叶级数的和函数；(2)证明：1/n2 =π2/6.

设f(x)为周期为2的周期函数，且f(x)=1-x,x∈[0,1]，若f(x)=a0/2+ancosnπx，则a2n =________.

设f(x)是周期为2的周期函数，它在区间(-1,1]上定义为f(x)=，则f(x)的傅里叶级数在x=1处收敛于______.

设函数f(x)=x2,0≤x<1，而S(x)=bnsinnπx,-∞<x<+∞，其中bn=2f(x)sinnπxdx,x=1,2,3,…，则S(-1/2)等于【】

将函数f(x)=2+|x|(-1≤x≤1)展开成以2为周期的傅里叶级数，并由此求级数1/n2 的和.

设f(x)=，则其以2π为周期的傅里叶级数在点x=π处收敛于__________.

设函数f(x)=πx+x2 (-π<x<π)的傅里叶级数展开式为a0/2+(ancosnx+bnsinnx)，其中系数b3的值为__________.

设f(x)=,S(x)=a0/2+ancosnπx,-∞<x<+∞，其中an=2f(x)cosnπxdx (n=0,1,2,…)，则S(-5/2)等于【】

已知f(x)=，将f(x)展开成正弦级数，并求该级数的和函数.

无穷级数

设R为幂级数anxn 的收敛半径，r是实数，则【】

设数列{an}满足a1=1,(n+1) an+1=(n+1/2) an，证明：当|x|<1时，幂级数an xn 收敛，并求其和函数.

证明：当x>0时，ln√x=1/(2n-1) ((x-1)/(1+x))2n-1 ，并讨论1/(2n-1) ((x-1)/(1+x))2n-1关于x∈(0,+∞)是否一致收敛.

已知数列{an}(an≠0)，若{an}发散，则【】

设非负函数f(x)在[0,+∞)上连续，给出以下三个命题：①若f² (x)收敛，则f(x)收敛.②若存在p>1，使得xp f(x)存在，则f(x)收敛.③若f(x)收敛，则存在p>1，使得xp f(x)存在.其中真命题个数为【】

已知幂级数anxn的和函数为ln⁡(2+x)，则na2n =【】

已知函数f(x)=x+1，若f(x)=a0/2+ancosnx,x∈[0,π]，则n²sina2n-1 =______.

求级数sinnx/n!=________.

设级数an 绝对收敛，bn 收敛，且an =A,bn =B，令cn=a1bn+a2bn-1+⋯+an b1=akbn-k+1，则cn =AB.

设函数f1 (x)在[0,1]上连续，K(x,y)在[0,1]×[0,1]上连续，对任意x∈[0,1]，定义fn+1(x)=K(x,y) fn (y)dy,n=1,2,⋯证明：函数列{fn (x)}在[0,1]上一致收敛于0.