设X1,X2,…,X16为来自总体N(μ,4)的简单随机样本.考虑假设检验问题:H0:μ≤10,H1:μ>10.Φ(x)表示标准正态分布函数,若该检验问题的拒绝域为W={X ̅≥11},其中X ̅=1/16·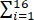 Xi ,则μ=11.5时,该检验犯第二类错误的概率为【 】
Xi ,则μ=11.5时,该检验犯第二类错误的概率为【 】
A、1 - Φ(0.5)
B、1 - Φ(1)
C、1 - Φ(1.5)
D、1 - Φ(2)
设X1,X2,…,X16为来自总体N(μ,4)的简单随机样本.考虑假设检验问题:H0:μ≤10,H1:μ>10.Φ(x)表示标准正态分布函数,若该检验问题的拒绝域为W={X ̅≥11},其中X ̅=1/16·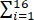 Xi ,则μ=11.5时,该检验犯第二类错误的概率为【 】
Xi ,则μ=11.5时,该检验犯第二类错误的概率为【 】
A、1 - Φ(0.5)
B、1 - Φ(1)
C、1 - Φ(1.5)
D、1 - Φ(2)
B
设A,B为随机事件,且0<P(B)<1,下列命题中为假命题的是【 】
已知α1=,α2=,α3=,记β1=α1,β2=α2 - kβ1,β3=α3 - l1 β1 - l2 β2,若β1,β2,β3 两两正交,则l1,l2依次为【 】
二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【 】
设函数f(x)在区间[0,1]上连续,则f(x)dx=【 】
设函数f(x)=sinx/(1+x2)在x=0处的3次泰勒多项式为ax+bx2+cx3,则【 】
设函数f(x,y)可微,且f(x+1,ex)=x(x+1)2 , f(x,x2)=2x2lnx,则df(1,1)=【 】
已知 fn(x)=求证:(1)对于任何自然数n,方程fn(x)=在区间(0,)中仅有一根;(2)设xn∈(0,)满足fn(xn)=,则.
设X1,X2为来自总体N(μ,σ2)的简单随机样本,其中σ(σ>0)是未知参数.若σ ̂=a|X1-X2 |为σ的无偏估计,则a=【 】
已知二次型f(x1,x2,x3 )=2x12+3x22++3x32+2ax2 x3 (a>0)通过正交变换化成标准形f=y12+2y22+5y32,求参数a及所用的正交变换矩阵.
设u=f(x,y,z),φ(x2,ey,z)=0,y=sinx,其中f,φ都具有一阶连续偏导数,且∂φ/∂z≠0,求du/dx.
函数u=ln(x+)在A(1,0,1)处沿A点指向B(3,-2,2)点方向的方向导数为________.
设直线l:在平面π上,且平面π与曲面z=x2+y2相切于点(1,-2,5),求a,b的值.
已知二次曲面方程x2+ay2+z2+2bxy+2xz+2yz=4,可以经过正交变换=P化为椭圆柱面方程η2+4ζ2=4,求a,b的值和正交矩阵P.
设曲线y=y(x)(x>0)经过点(1,2),该曲线上任一点P(x,y)到y轴的距离等于该点处的切线在y轴上的截距.(Ⅰ)求y(x);(Ⅱ)求函数f(x)=y(t)dt在(0,+∞)上的最大值.
设f(x)在[0,1]上具有二阶导数,且满足条件|f(x)|≤a,|f''(x)|≤b,其中a,b都是非负常数,c是(0,1)内任意一点,证明:|f'(c)|≤2a+b/2.
对数螺线ρ=eθ在点(ρ,θ)=(eπ/2,π/2)处的切线的直角坐标方程为__________.
设函数f(u)具有二阶连续导数,而z=f(exsiny)满足方程∂2z/∂x2+∂2z/∂y2=e2x z,求f(u).
设总体X的概率密度为f(x)=,其中θ>-1是未知参数.X1,X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.