已知 fn(x)=
求证:(1)对于任何自然数n,方程fn(x)= 在区间(0,
在区间(0, )中仅有一根;
)中仅有一根;
(2)设xn∈(0, )满足fn(xn)=
)满足fn(xn)= ,则
,则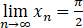 .
.
已知 fn(x)=
求证:(1)对于任何自然数n,方程fn(x)= 在区间(0,
在区间(0, )中仅有一根;
)中仅有一根;
(2)设xn∈(0, )满足fn(xn)=
)满足fn(xn)= ,则
,则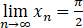 .
.
(1)已知fn(x)=1-(1-cosx)n∈C[0,],且fn(0)=1,fn()=0,则由介值定理知,对于∈(0,1),存在xn∈(0,),使得fn(xn)=,又(x)=-n(1-cosx)n-1sinx<0,x∈(0,)因此fn(x)在(0...
查看完整答案