求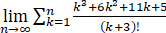 
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（1977年莫斯科民族友谊大学）
答案解析
暂无答案
讨论
验证函数f(x)=lnx在区间[1,+∞)上一致连续，但在(0,1)上不一致连续.
证明：f(x)=tx-1 e-t lntdt 在(0,+∞)上连续.
设f(x)在x=0处连续，且对任意的x∈R，有f(x)=f(3x)，证明：f(x)是常值函数.
已知φ(x)=|x-t|f(t)dt，若积分存在，且f(x)>0，证明：φ(x)为[a,b]上的凸函数.
当x→0时，函数f(x)=ax+bx2+ln(1+x)与g(x)=ex^2 -cosx是等价无穷小，则ab=______.
已知{xn },{yn}满足x1=yn=1/2,xn+1=sinxn,yn+1=yn2 (n=1,2,⋯) ，则当n→∞时【 】
给定x0>0以及[0,+∞)上连续函数f(x)，证明：至多具有一个定义于[0,+∞)上的连续函数y(x)满足对任意的x>0，有dy/dx=-y³+f(x)，其中y(0)=y0.